6.4 Volume of a Solid: Slicing MethodPrinted Page 433
433
OBJECTIVES
When you finish this section, you should be able to:
In Sections 6.2 and 6.3, we found the volumes of solids of revolution obtained by revolving a region about a line. We now investigate a method, called slicing, to find the volume of a solid that is not necessarily a solid of revolution.
1 Use the Slicing Method to Find the Volume of a SolidPrinted Page 433
The idea behind the slicing method is to cut a solid into thin slices using planes perpendicular to an axis and then to add the volumes of all the slices to obtain the total volume of the solid. The slicing method relies on the fact that the area of each cross section obtained by slicing can be expressed as a function of the position of the slice. See Figure 38.
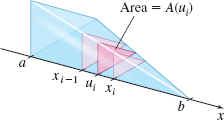
We begin by partitioning the interval [a,b] on the x-axis into n subintervals: [a,x1], [x1,x2],…,[xi−1,xi],…,[xn−1,b]
each of width Δx=b−an. In the ith subinterval, we select a number ui and slice through the solid at x=ui using a plane that is perpendicular to the x-axis. Suppose the area of the cross section that results is A(ui).
The volume Vi of the thin slice from xi−1 to xi is approximately Vi=A(ui)Δx, and the sum of the volumes from each subinterval is n∑i=1Vi=n∑i=1 [A(ui)Δx]
IN WORDS
The volume Vi of a slice is Vi=(Area of cross section) (Thicknessof the slice)=A(ui)Δx
These sums approximate the volume V of the solid from x=a to x=b. As the number n of subintervals increases, the sums n∑i=1Vi=n∑i=1[A(ui)Δx] become better approximations to the volume V of the solid. These sums are Riemann sums. So, if the cross sections A(ui) vary continuously with x, then the limit is a definite integral.
Volume of a Solid Using the Slicing Method
If for each x in [a,b], the area A(x) of the cross section of a solid is known and is continuous on [a,b], then the volume V of the solid is \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=\int_{a}^{b}A(x)~{\it dx}}\tag{1} \end{align*}
NEED TO REVIEW?
Geometry formulas are discussed in Appendix A.2, p. A-15.
The key behind the slicing method is that when the solid is sliced at any number x, the area of the slice is a function of x. For example, if all parallel cross sections of the solid have the same geometric shape (all are semicircles, or triangles, or squares, etc.), then the area of each cross section can be expressed as a function A(x), and the volume of the solid can be found using (1).*
*To find the volume of most solids requires the use of a double integral or a triple integral (the subjects of Chapter 14).
434
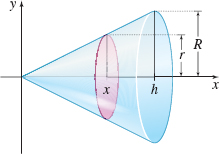
EXAMPLE 1Using the Slicing Method to Find the Volume of a Cone
Use the slicing method to verify that the volume of a right circular cone having radius R and height h is V=\dfrac{1}{3}\pi R^{2}h.
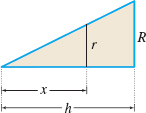
Solution We position the cone with its vertex at the origin and its axis on the x-axis, as shown in Figure 39.
The cone extends from x=0 to x=h. The cross section at any number x is a circle. To obtain its area A, we need the radius r of the circle. Embedded in Figure 39 are two similar triangles, one with sides x and r; the other with sides h and R, as shown in Figure 40. Because these triangles are similar (AAA), corresponding sides are in proportion. That is, \begin{eqnarray*} \dfrac{r}{x} &=&\dfrac{R}{h} \\[6pt] r &=&\dfrac{R}{h}x \end{eqnarray*}
So, r is a function of x and the area A of the circular cross section is \begin{equation*} A=A(x)=\pi [ r(x)] ^{2}=\pi\! \left( \dfrac{R}{h}x\right) ^{2}= \dfrac{\pi R^{2}}{h^{2}}x^{2} \end{equation*}
NEED TO REVIEW?
Similar triangles are discussed in Appendix A.2, pp. A-13 to A-14.
Since A is a continuous function of x (where the slice was made), we can apply the slicing method. The volume V of the right circular cone is \begin{equation*} V = \int_{a}^{b}A(x)~{\it dx}=\displaystyle \int_{0}^{h}\frac{\pi R^{2}}{h^{2}}x^{2}~{\it dx}=\frac{\pi R^{2}}{h^{2}}\!\displaystyle \int_{0}^{h}x^{2}~{\it dx}\\[11pt] = \frac{\pi R^{2}}{h^{2}}\left[ \frac{x^{3}}{ 3}\right] _{0}^{h}=\frac{\pi R^{2}h}{3} ~\hbox{cubic units} \end{equation*}
NOTE
A right circular cone is a solid of revolution, so the formula for its volume also can be verified using the disk method.
NOW WORK
In Example 1, the cone was positioned so that its axis coincided with the x-axis and its vertex was at the origin. The way in which a solid is positioned relative to the x-axis is important if the area A of the slice is to be easily found, expressed as a function of x, and integrated.
EXAMPLE 2Using the Slicing Method to Find the Volume of a Solid
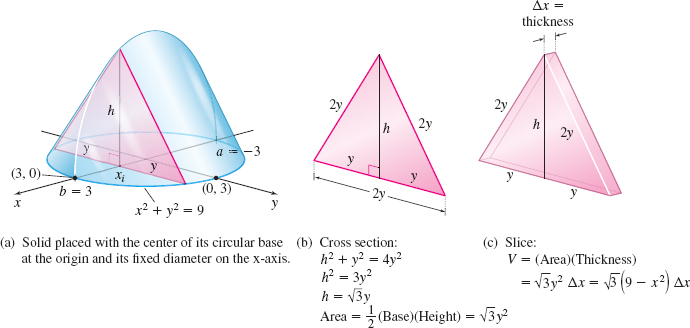
A solid has a circular base of radius 3 units. Find the volume V of the solid if every plane cross section that is perpendicular to a fixed diameter is an equilateral triangle.
Solution Position the circular base so that its center is at the origin, and the fixed diameter is along the x-axis. See Figure 41(a). Then the equation of the circular base is x^{2}+y^{2}=9. Each cross section of the solid is an equilateral triangle with sides = 2y, height h, and area A=\sqrt{3}y^{2}. See Figure 41(b). Since y^{2}=9-x^{2}, the volume V_i of a typical slice is V_{i}=\hbox{(Area of the cross section)(Thickness)}=A(x_{i})~\Delta x=\sqrt{3 }\left( 9-x_{i}^{2}\right) \Delta x as shown in Figure 41(c).
435
The volume V of the solid is \begin{eqnarray*} V&=&\int_{a}^{b}A(x)~{\it dx}=\int_{-3}^{3}\sqrt{3}(9-x^{2})~{\it dx} \underset{\underset{\underset{\color{#0066A7}{\hbox{an even function.}}}{\color{#0066A7}{\hbox{The integrand is}}}} {\color{#0066A7}{\uparrow }}} {=}2\sqrt{3}\int_{0}^{3}(9-x^{2})~{\it dx}=2\sqrt{3}\left[ 9x-\frac{ x^{3}}{3}\right] _{0}^{3}\\[-10pt] &=&36\sqrt{3}\hbox{ cubic units} \end{eqnarray*}
NEED TO REVIEW?
Even and odd functions are discussed in Section P.1, pp. 9-10, and the integrals of even and odd functions are discussed in Section 5.6, pp. 393-394.
NOW WORK
EXAMPLE 3Using the Slicing Method to Find the Volume of a Pyramid
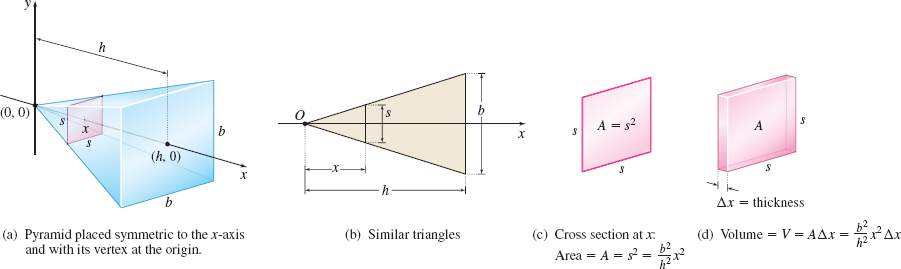
Find the volume V of a pyramid of height h with a square base, each side of length b.
Solution We position the pyramid with its vertex at the origin and its axis along the positive x-axis. Then the area A of a typical cross section at x is a square. Let s denote the length of the side of the square at x. See Figure 42(a). We form two triangles: one with height x and side s, the other with height h and side b. These triangles are similar (AAA), as shown in Figure 42(b). Then we have \begin{equation*} \dfrac{x}{s}=\dfrac{h}{b}\qquad\hbox{ or }\qquad s =\dfrac{b}{h}x \end{equation*}
436
So, s is a function of x, and the area A of a typical cross section is A=s^{2}=\dfrac{b^{2}}{h^{2}}x^{2}. See Figure 42(c). The volume V of a typical cross section is V=\dfrac{ b^{2}}{h^{2}}x^{2}\Delta x. See Figure 42(d).
Since A is a continuous function of x, where the slice occurred, we have \begin{equation*} V=\int_{0}^{h}A(x) \,{\it dx}=\displaystyle \int_{0}^{h}\dfrac{b^{2}}{h^{2}} x^{2}{\it dx}= \frac{b^{2}}{h^{2}}\int_{0}^{h}x^{2}{\it dx}=\frac{b^{2}}{h^{2}} \left[ \frac{x^{3}}{3} \right] _{0}^{h}=\frac{1}{3}b^{2}h\hbox{ cubic units} \end{equation*}
NOW WORK
In each example we have done so far, the base has been a recognizable geometric shape. The slicing method can also be used to find the volume of a solid with an irregular base, provided information about the slices of the solid is known.
EXAMPLE 4Using the Slicing Method to Find the Volume of a Solid
Find the volume V of the solid whose base is the region bounded by the graphs of y=\sqrt{x} and y=\dfrac{1}{8}x^{2}, if slices perpendicular to the base along the x-axis have cross sections that are squares.
Solution We begin by graphing the region bounded by the graphs of y=\sqrt{x} and y=\dfrac{1}{8}x^{2}, as shown in Figure 43. The points of intersection of the two graphs are found by solving the equation \begin{eqnarray*} \sqrt{x} &=&\dfrac{1}{8}x^{2} \\[2pt] x &=&\dfrac{1}{64}x^{4} \\[2pt] x^{4}-64x &=&0 \\[2pt] x( x^{3}-64) &=&0 \\[2pt] x &=&0 \quad\hbox{or}\quad x=4 \end{eqnarray*}
The two graphs intersect at the points \left( 0,0\right) and (4,2).
The solid with slices perpendicular to the base along the x-axis that are squares is shown in Figure 44(a). See Figure 44(b). A slice perpendicular to the x-axis at x_{i} is a square with side s_{i}=\displaystyle\sqrt{x_{i}}-\dfrac{1}{8}x_{i}^{2}. The area A_{i} of the cross section at x_{i} is A_{i}=s_{i}^{2}=\left( \sqrt{x_{i}}-\dfrac{1}{8} x_{i}^{2}\right) ^{2}
437
See Figure 44(c). The volume V_{i} of a typical slice is \begin{eqnarray*} V_{i}&=& \hbox{(Area of the cross section)(Thickness of the slice)}\\[3pt] &=&A (x_{i}) \Delta x=\left( \sqrt{x_{i}}-\dfrac{1}{8}x_{i}^{2}\right) ^{2}\Delta x \end{eqnarray*}
The volume V of the solid is \begin{eqnarray*} V &=&\int_{0}^{4}A(x) {\it dx}=\int_{0}^{4}\left( \sqrt{x}-\dfrac{1}{8} x^{2}\right) ^{2}{\it dx}=\int_{0}^{4}\left( x-\dfrac{1}{4}x^{5/2}+\dfrac{1}{64} x^{4}\right) {\it dx} \notag \\[5pt] &=&\left[ \dfrac{x^{2}}{2}-\dfrac{1}{14}x^{7/2}+\dfrac{1}{320}x^{5}\right] _{0}^{4}=8-\dfrac{128}{14}+\dfrac{1024}{320}=\dfrac{72}{35}\hbox{ cubic units } \end{eqnarray*}