Chapter 14
Section 14.1
1. True
2. False
3. (d)
4. True
5. (a) 36
(b) 9
7. (a) 60
(b) 164
9. 320
11. x
13. 
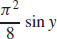
15. e − 1
17. 
19. 27
21.
23. 0
25. 
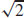
27. 
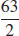
29. e − 1
31. 0
33. 1 + e2
35. 
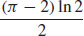
37. 30
39. 28
41. 5(1 − e)
43. 
45. 
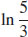
47. 
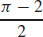
49. 
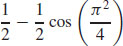
51. 
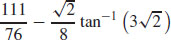
53. 
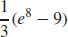
55. 5 cubic units
57. 
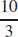cubic units
59. 1 cubic unit
61. 3 ln 2 cubic units
63. (e − 1)2(e + 1) cubic units
65. 
cubic units
67. See the Student Solutions Manual.
69. 
Section 14.2
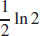
1. x-simple region
2. True
3. True
4. Answers will vary.
5. (a)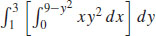 
(b)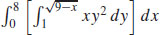 
(c)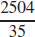 
7. (a)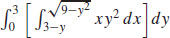 
(b)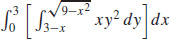 
(c)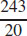 
9. 
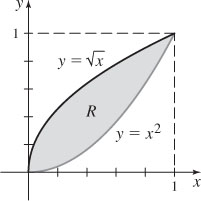
11. 
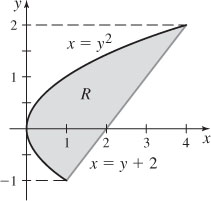
13. 1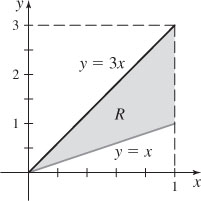
15.
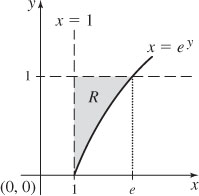
17. 6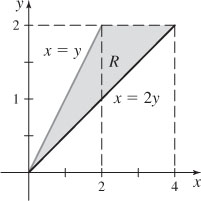
19. 
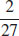
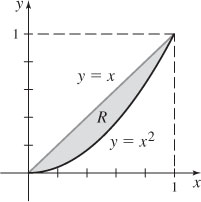
21. 
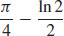
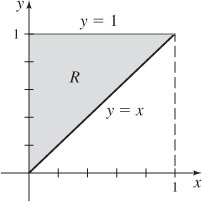
23. 
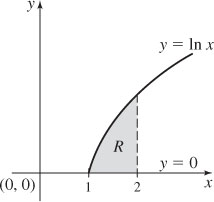
25. 
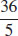
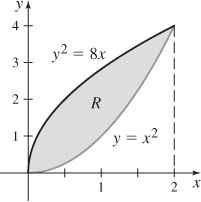
27. 
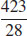
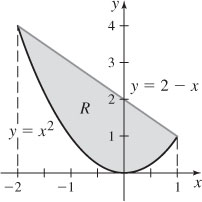
29. 
square units
31. A = 72 square units
33. A = 2 square units
35. 
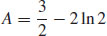square units
37. 
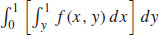
39. 
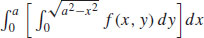
41. 
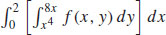
43. 
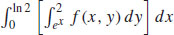
45. 14
47. 0
49. 
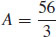square units
51. 
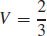cubic units
53. 
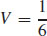cubic units
55. V = 8π cubic units
57. 
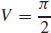cubic units
59. 
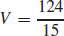cubic units
61. (a)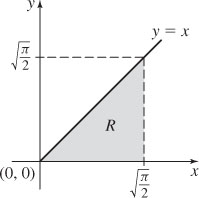 
(b) 
(c) 
63. (a)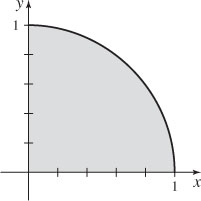 
(b)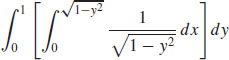 
(c) 1
65. (a) 
(b)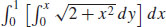 
(c)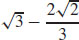 
67. (a)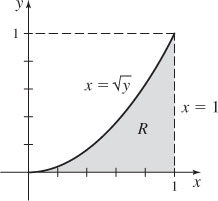 
(b)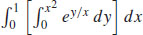 
(c)
69. 
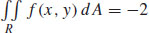
71. 
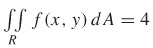
73. The solid is the volume under the hemisphere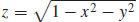 
in the first octant.
75. The solid is a rectangular box with height z = 3 units, with a rectangular base of dimensions x = 4 units and y = 1 unit.
77. (a) 0
(b) 
79. (a)
(b)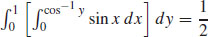 
81. 
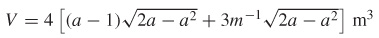
83. Answers will vary.
85. 4
87. 12 − 4e
89. See the Student Solutions Manual.
Section 14.3
1. f (r, θ) = 2r
2. r dr dθ
3. False
4. True
5. 
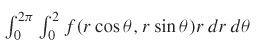
7. 
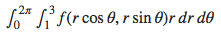
9. 
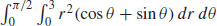
11. 
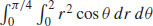
13. 
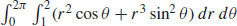
15. 
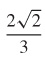
17. 
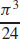
19. 
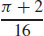
21. 0
23. 6
25.
27. 0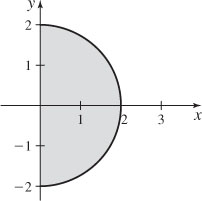
29. 
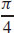
31. 4π
33. 
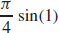
35. 
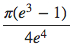
37. 
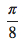
39. 21π
41. 
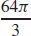
43. 
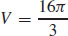cubic units
45. 
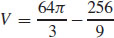cubic units
47. 
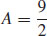square units
49. 
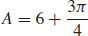square units
51. 
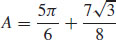square units
53. 
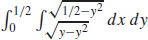
55. 
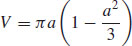cubic meters
57. (a)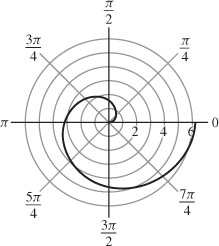 
(b)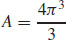 
square units
59. 
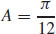square units.
61. (a) See the Student Solutions Manual.
(b) See the Student Solutions Manual.
(c)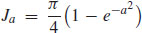 
(d) See the Student Solutions Manual.
(e) See the Student Solutions Manual.
Section 14.4
1. Mass
2. False
3. 
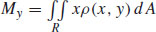
4. False
5. True
6. False
7. 
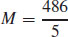and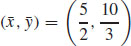 
9. M = 64 and 
11. 
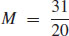and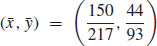 
13. 
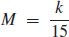, where k is the constant of proportionality, and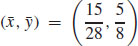 
15. M = 5k, where k is the constant of proportionality, and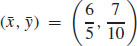 
17. 
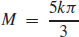, where k is the constant of proportionality, and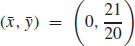 
19. 
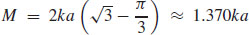, where k is the constant of proportionality, and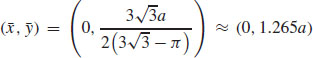 
21. Ix = 2ρ
23. 
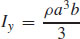
25. 
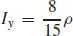
27. M = 2πk ln 2, where k is the constant of proportionality
29. M = ka(π − 2) ≈ 1.142ka, where k is the constant of proportionality, and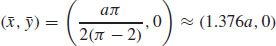 
31. 
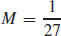
33. 
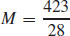and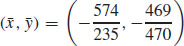 
35. 
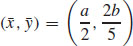
37. (a)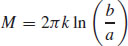 
, where k is the constant of proportionality. As a → 0+, M →∞.
(b) I = kπ(b2 − a2), where k is the constant of proportionality. As a → 0+, I → kπb2.
39. See the Student Solutions Manual.
41. See the Student Solutions Manual.
43. (a) See the Student Solutions Manual.
(b)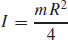 
(c)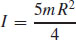 
Section 14.5
1. True
2. False
3. S = 3π
5. 
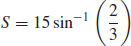
7. 
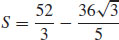
9. 
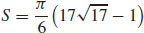
11. 
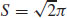
13. 
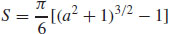
15. S = 8π
17. 
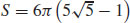
19. 
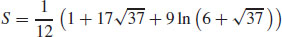
21. 
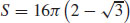
23. (a) 
(b) S ≈ 55.436
25. See the Student Solutions Manual.
27. See the Student Solutions Manual.
29. \(S = 2 R^2 (\pi - 2)\) square units
Section 14.6
1. True
2. False
3. True
4. False
5.
7. 1
9. e − 1
11. 
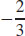
13. 81
15. 2(e − 2)
17. 
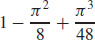
19. 
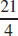
21. 
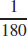
23. 
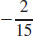
25. −0.4142
27. 
29. 
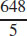
31. (a) The semi-cylinder is given by x2 + y2 = 4 and the planes x = 0, z = 0, and z = 1.
(b)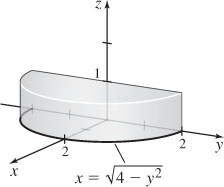
33. (a) The solid is bounded by y = x2 and the planes z = 0, x = 1, and z = y.
(b)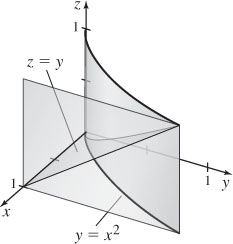
35. 
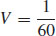cubic units
37. 
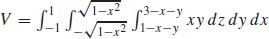cubic units
39. 
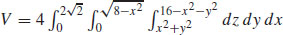cubic units
41. 
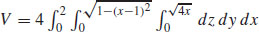cubic units
43. M = ka5, where k is the constant of proportionality
45. 
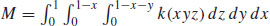, where k is the constant of proportionality
47. 
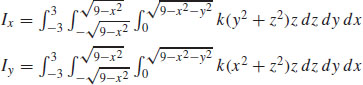, where k is the constant of proportionality
49. 
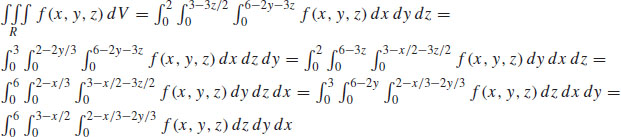
51. See the Student Solutions Manual. When a = b = c, the formula for the volume of an ellipsoid reduces to the formula for the volume of a sphere.
53. V = 2 cubic units
55. See the Student Solutions Manual.
Section 14.7
1. x = r cos θ, y = r sin θ, and z = z
2. r = 2z
3. dV = r dr dθ dz
4. True
5. 
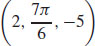
7. 
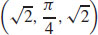
9. (2, 0, 4)
11. 
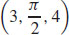
13. 
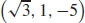
15. (1, 0, 8)
17. (0, 2, 0)
19. The triple integral represents the volume of a hemisphere of radius 1 to the right of the xz-plane, that is y ≥ 0.
21. The triple integral represents the volume inside the vertical cylinder x2 + y2 = 4, bounded below by the xy-plane and bounded above by the surface of the cone 
.
23. 
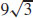
25. 
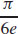
27. 24π
29. 0
31. 0
33. 
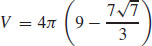cubic units
35. V = 64π cubic units
37. 
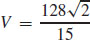cubic units
39. 
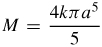, where k is the constant of proportionality
41. 
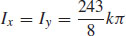, where k is the constant of proportionality
43. 
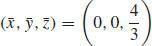
45. 
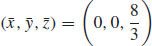
47. 
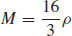
49. 
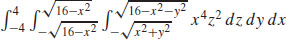
51. (a)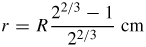 
(b) r ≈ 6.083 cm
53. 
Section 14.8
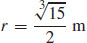
1. Origin
2. z-axis
3. False
4. True
5. dV = ρ2 sin ϕ dρ dθ dϕ
6. Sphere
7. 
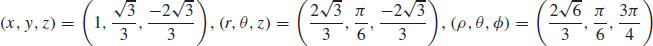
9. 
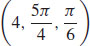
11. 
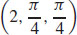
13. 
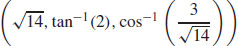
15. 
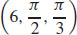
17. 
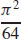
19. 
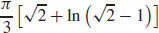
21. 0
23. 
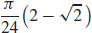
25. 
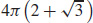
27. 
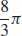
29. 
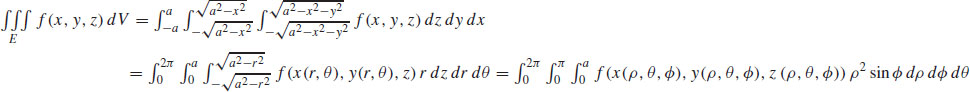
31. 
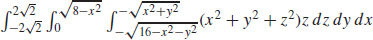
33. 18π and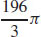 
35. 
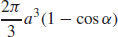
37. 
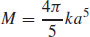, where k is the constant of proportionality
39. 
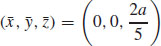
41. 
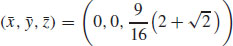
43. 
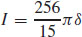, where δ is the mass density
45. 
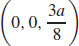
47. (a) k = 1.238 × 10−6 m−1 and D0 = 2500 kg/m3
(b) The calculated mass of Dione is 1.10 × 1021 kg, which differs from the measured mass by only 4.76%. The density model for the asteroid is reasonable.
49. See the Student Solutions Manual.
Section 14.9
1. 
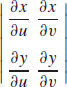
2. True
3. 
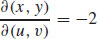
5. 
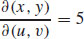
7. 
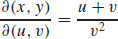
9. 
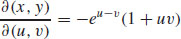
11. 
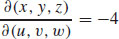
13. 
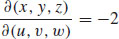
15. 
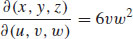
17. A = 6π square units
19. (a)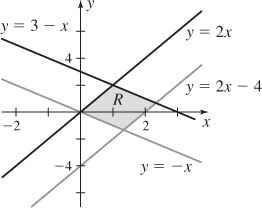 
(b)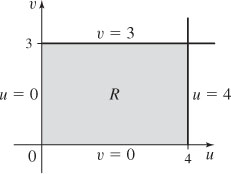 
(c)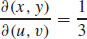 
(d)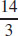 
21. (a)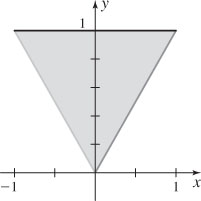 
(b)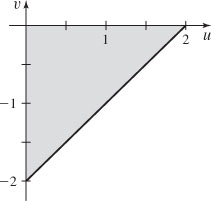 
(c) 
(d) 0
23. 0
25. 16π
27. (a) 
(b) 
(c)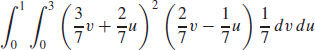 
(d)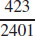 
29. (a)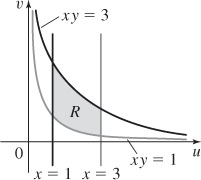 
(b)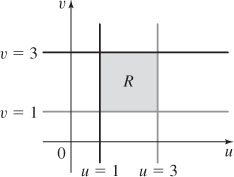 
(c)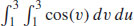 
(d) 2(sin 3 − sin 1)
31. 
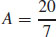square units
33. V = 36 cubic units
35. 
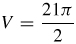cubic units
37. See the Student Solutions Manual.
Review Exercises
1.
3. 
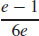
5. 
7. (a) The midpoint Riemann sum is 32.
(b) The largest Riemann sum is 80, the lowest Riemann sum is −16, and their average is 32.
(c) 32
9. 
11. V = 6 cubic units
13. 
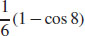
15. V = 6 cubic units
17. 
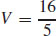cubic units
19. 
21. A = π square units
23. M = 104k, where k is the constant of proportionality
25. 
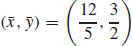
27. 
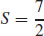
29. 
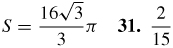
31. 
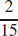
33. 
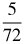
35. 
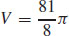cubic units
37. (a) (r, θ, z) = (3, 0, 4)
(b)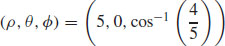 
39. (a)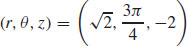 
(b)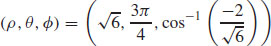 
41. 
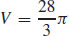cubic units
43. 
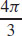
45. 
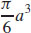
47. 
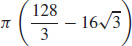
49. 16π
51. 
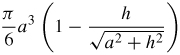
53. 
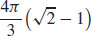
55. 
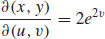
57. 
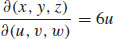
59. 203
61. 0