14.5 Surface Area
OBJECTIVE
When you finish this section, you should be able to:
- Find the surface area that lies above a region \(R\) (p. 938)
So far we have used a double integral to find the volume under a surface \( z=f(x, y) \ge 0\) and above a closed, bounded region \(R\) of the \( xy\)-plane. In this section, we use a double integral to find the surface area of \(z=f(x, y) \ge 0\) above a closed, bounded region \(R.\) In developing the formula for surface area, we use tangent planes to approximate surface area.
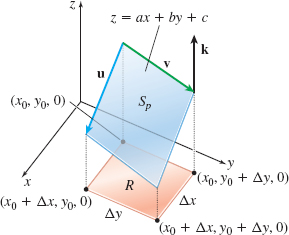
We begin with the simple case where the surface is a plane \(z=ax+by+c\) and the region \(R\) is a rectangle with sides of lengths \(\Delta x\) and \(\Delta y\) . The surface area \(S_{p}\) is the area of the part of the plane that lies above the rectangle, in this case, a parallelogram, as shown in Figure 36. Notice that this parallelogram is the intersection of the plane and the cylinder formed by projecting the perimeter of the rectangle with sides \(\Delta x\) and \(\Delta y \) vertically upward.
The adjacent sides of the parallelogram are given by the vectors \(\mathbf{u}\) and \(\mathbf{v}\). Both \(\mathbf{u}\) and \(\mathbf{v}\) have the same initial point \(( x_{0}, y_{0},ax_{0}+by_{0}+c) \) on the parallelogram. The terminal point of \(\mathbf{u}\) is \(( x_{0}+\Delta x, y_{0}, a( x_{0}+\Delta x) +by_{0}+c) \) and the terminal point of \(\mathbf{v }\) is \(( x_{0}, y_{0}+\Delta y, ax_{0}+b( y_{0}+\Delta y) +c).\) So, \(\mathbf{u}\) and \(\mathbf{v}\) are given by \[ \mathbf{u}=\Delta x\mathbf{i}+a\Delta x\mathbf{k},\qquad \mathbf{v}=\Delta y\mathbf{j}+b\Delta y\mathbf{k} \]
NEED TO REVIEW?
Vectors are discussed in Section 10.2, pp. 699-702, and properties of the cross product are discussed in Section 10.5, pp. 724-730.
The area of the parallelogram is \begin{eqnarray*} \Vert \mathbf{u}\times \mathbf{v}\Vert &=&\left\Vert \Delta x(\mathbf{i}+a \mathbf{k})\times \Delta y(\mathbf{j}+b\mathbf{k})\right\Vert =\left\Vert ( \mathbf{i}+a\mathbf{k})\times (\mathbf{j}+b\mathbf{k})\right\Vert \Delta x\Delta y\\[4pt] &=&\left\Vert -a\mathbf{i}-b\mathbf{j}+\mathbf{k}\right\Vert \Delta x\Delta y=\sqrt{a^{2}+b^{2}+1}\ \Delta x\Delta y \end{eqnarray*}
Let \(R\) be a closed rectangular region in the \(xy\)-plane with sides of length \(\Delta x\) and \(\Delta y\). If the perimeter of \(R\) is projected upward parallel to the \(z\)-axis, the result is a cylinder. Let \(S_{p}\) denote the area cut from the plane \(z=ax+by+c\) by this cylinder. Then the area \(S_{p}\) is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ S_{p}=\sqrt{a^{2}+b^{2}+1}\ \Delta x \Delta y}\tag {1} \]
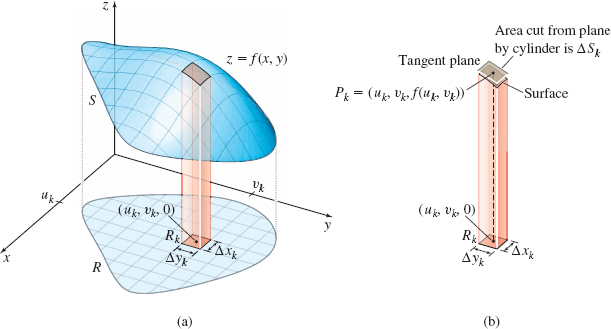
We now develop a formula for the surface area of the graph of a nonnegative function \(z=f(x, y)\) that is defined over a closed, bounded region \(R\). We assume that \(f\) has first-order partial derivatives that are continuous at every point of the region \(R\).
See Figure 37(a). Using lines parallel to the \(x\)- and \(y\)-axes, we partition \(R\) into \(N\) rectangles and consider the \(k\)th rectangle \(R_{k}\) having area \(A_{k}\). Now we select a point \((u_{k},v_{k})\) in \(R_{k}\) and construct the tangent plane to the surface at the corresponding point \( P_{k}=(u_{k},v_{k},f(u_{k},v_{k}))\) on the surface. See Figure 37(b). The equation of this tangent plane can be written as \[\bbox[5px, border:1px solid black, #F9F7ED]{ z=f_{x}(u_{k},v_{k})(x-u_{k})+f_{y}(u_{k},v_{k})(y-v_{k})+f(u_{k},v_{k}) }\tag {2} \]
937
The perimeter of the rectangle \(R_{k},\) when it is projected upward parallel to the \(z\)-axis, results in a cylinder. Let \(\Delta S_{k}\) denote the area cut from the tangent plane at \(P_{k}\) by the cylinder. The number \(\Delta S_{k}\) is an approximation to the surface area of the part of the surface that lies above the \(k\)th rectangle \(R_{k}\). By adding the \(N\) areas and taking the limit of the sums as the norm \(\left\Vert P\right\Vert \) of the partition approaches \(0\), we obtain the surface area \(S\) of the part of the surface \(z=f(x, y)\) that lies above the region \(R.\) \[ S=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{k=1}^{N}\Delta S_{k}\tag{3} \]
To obtain a formula for \(\Delta S_{k}\), we combine (2), the equation of the tangent plane to the surface at the point \(P_{k},\) \[ \begin{equation*} z=f_{x}(u_{k},v_{k})(x-u_{k})+f_{y}(u_{k},v_{k})(y-v_{k})+f(u_{k},v_{k})\qquad {\color{#0066A7}{\hbox{Equation (2)}}} \end{equation*} \]
and formula (1) for the surface area \(S_{p}\) of a plane \(z=ax+by+c\) \[ S_{p}=\sqrt{a^{2}+b^{2}+1}\,\Delta x\Delta y\qquad{\color{#0066A7}{\hbox{Formula (1)}}} \]
The result is \begin{equation*} \Delta S_{k}=\sqrt{[f_{x}(u_{k},v_{k})]^{2}+[f_{y}(u_{k},v_{k})]^{2}+1} \,\Delta A_{k} \end{equation*}
Now we substitute this expression for \(\Delta S_{k}\) into (3) to obtain the surface area \(S\) of the part of the surface that lies above the region \(R\). Then \[ S=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{k=1}^{N}\displaystyle\sqrt{ [f_{x}(u_{k},v_{k})]^{2}+[f_{y}(u_{k},v_{k})]^{2}+1}\,\Delta A_{k} \]
Since the first-order partial derivatives of \(f\) are continuous on \(R,\) the limit exists and \(S\) is a double integral.
Surface Area Above a region \(R\)
Let \(z=f(x, y)\) be a function of two variables defined on a closed, bounded region \(R\). If \(f_{x}\) and \(f_{y}\) are continuous on \(R\), then the surface area \(S\) of the part of the surface that lies above \(R\) is given by \[\bbox[5px, border:1px solid black, #F9F7ED]{ S=\displaystyle\iint\limits_{\kern-3ptR}\displaystyle\sqrt{ [f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}\, {\it dA} } \]
1 Find the Surface Area That Lies Above a Region R
938
Finding Surface Area
Find the surface area of the part of the surface \(z=f(x, y)=\dfrac{2}{3} (x^{3/2}+y^{3/2})\) that lies above the region \(R,\) a rectangle enclosed by the lines \(x=0\), \(x=1\), \(y=0\), and \(y=2\).
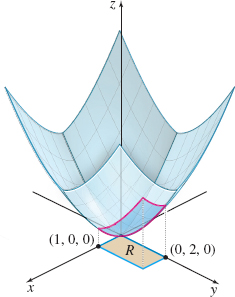
Solution Figure 38 shows the surface \(z=f(x, y)=\dfrac{2}{3} (x^{3/2}+y^{3/2})\) and the surface area \(S\) above the rectangle \(R\). We begin by finding the partial derivatives of \(z=f(x, y)\): \[ f_{x}(x,y)=x^{1/2} \qquad f_{y}(x,y)=y^{1/2} \]
Since \(f_x\) and \(f_y\) are continuous on \(R\), the surface area \(S\) above \(R\) is \begin{eqnarray*} S &=&\displaystyle\iint\limits_{\kern-3ptR}\sqrt{[f_{x}(x, y)]^{2}+[f_{y}(x,y)]^{2}+1} \,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{( x^{1/2}) ^{2}+( y^{1/2}) ^{2}+1}\,{\it dA} \notag \\ &=& \int_{0}^{1}\int_{0}^{2}\sqrt{x+y+1}\,{\it dy}\,{\it dx}=\int_{0}^{1}\left[ \dfrac{2}{3 }(x+y+1)^{3/2}\right] _{0}^{2}\,{\it dx} \notag \\ &=&\dfrac{2}{3}\int_{0}^{1}\big[ (x+3)^{3/2}-(x+1)^{3/2}\big] \,{\it dx}=\left( \dfrac{2}{3}\right) \left( \dfrac{2}{5}\right) \big[ (x+3)^{5/2}-(x+1)^{5/2}\big] _{0}^{1} \notag \\ &=&\dfrac{4}{15}( 32-9\sqrt{3}-4\sqrt{2}+1) = \dfrac{4}{15} (33-9\sqrt{3}-4\sqrt{2}) \end{eqnarray*}
NOW WORK
Problem 5.
Finding Surface Area
Find the surface area of the part of the paraboloid \(z=f(x,y)=1-x^{2}-y^{2}\) that lies above the \(xy\)-plane.
Solution Figure 39 shows the part of the surface \(z=1-x^{2}-y^{2}\) that lies above the \(xy\)-plane and its projection onto the \(xy\)-plane, the region \(R\) enclosed by the circle \(x^{2}+y^{2}=1\). We begin by finding the partial derivatives of \(z=f(x,y)\). \[ f_{x}(x,y)=-2x\qquad f_{y}(x,y)=-2y \]
Since \(f_x\) and \(f_y\) are continuous on \(R\), the surface area \(S\) of the part of \(z=f(x,y) =1-x^{2}-y^{2}\) that lies above \(R\) is \begin{eqnarray*} S&=&\displaystyle\iint\limits_{\kern-3ptR}\sqrt{[f_{x}(x,y)]^{2}+[f_{y} (x,y)]^{2} +1} \,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{ (-2x)^{2}+(-2y)^{2}+1}\,{\it dA}\\ &=&\displaystyle\iint\limits_{\kern-3ptR}\sqrt{4(x^{2}+y^{2})+1} \,{\it dA} \end{eqnarray*}
Since both the region \(R\) (a circle) and the integrand involve \(x^{2}+y^{2}\) , we use polar coordinates \((r,\theta)\). For the region \(R,\) we have \(0\leq r\leq 1\) and \(0\leq \theta \leq 2\pi\). Then \[ \begin{equation*} \begin{array}{rcl} S& =&\displaystyle\iint\limits_{\kern-3ptR}\sqrt{4(x^{2}+y^{2})+1}\,d\!A\underset{\underset{\underset{{\color{#0066A7}{\hbox {\({dx}\, {dy}=r\,{dr} d\theta\)}}}} {\color{#0066A7}{\hbox{\(x^{2}+y^{2}=r^{2}\)}}}} {\color{#0066A7}{\uparrow}}}{=} \int_{0}^{2\pi }\int_{0}^{1}\sqrt{4r^{2}+1}r\,dr\,d\theta \notag \\ &=&\int_{0}^{2\pi }\dfrac{1}{12}\big[ ( 4r^{2}+1) ^{3/2}\big] _{0}^{1}\,d\theta =\dfrac{1}{12}(5\sqrt{5}-1)\int_{0}^{2\pi }\,d\theta = \dfrac{1}{12}(5\sqrt{5}-1)2\pi\\[9pt] &=&\dfrac{\pi }{6}(5\sqrt{5}-1) \end{array} \end{equation*} \]
NOW WORK
Problem 9.
939
Finding Surface Area
Find the surface area of the part of the sphere \(x^{2}+y^{2}+z^{2}=a^{2}\) that lies above the \(xy\)-plane and is contained within the cylinder \( x^{2}+y^{2}=ax,\) \(a\gt 0\).
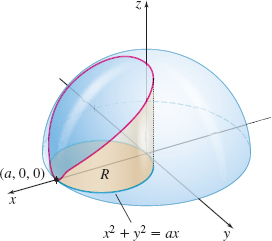
Solution Figure 40 shows the sphere and the cylinder. The equation of the surface in explicit form is \[ z=f(x,y)=\sqrt{a^{2}-x^{2}-y^{2}} \]
The partial derivatives of \(z\) \(=f(x,y)\) are \[ f_{x}(x,y)=-\dfrac{x}{\sqrt{a^{2}-x^{2}-y^{2}}}\qquad f_{y}(x,y)=- \dfrac{y}{\sqrt{a^{2}-x^{2}-y^{2}}} \]
The projection of the cylinder onto the \(xy\)-plane is the region \(R\) enclosed by the circle \(x^{2}+y^{2}=ax\), \(a\gt 0.\) Then the surface area \(S\) that we seek is \[ S=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{\dfrac{x^{2}}{a^{2}-x^{2}-y^{2}}+\dfrac{y^{2}}{ a^{2}-x^{2}-y^{2}}+1}\,\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}\sqrt{\dfrac{a^{2}}{ a^{2}-x^{2}-y^{2}}}\,{\it dA} \]
Since the integrand involves the expression \(x^{2}+y^{2}\) and the boundary of \(R\) is the circle \(x^{2}+y^{2}=ax\), we use polar coordinates \((r,\theta)\). We begin by finding the limits of integration. Since \begin{eqnarray*} x^{2}+y^{2} &=&ax \\ r^{2} &=&ar\cos \theta \\ r &=&a\cos \theta \end{eqnarray*}
we find that \(r\) varies from \(0\) to \(a\cos \theta\).
Since half the area is to the right of the \(xz\)-plane and half is to the left of the plane, we can let \(\theta\) vary from \(0\) to \(\dfrac{\pi }{2}\) and double the area. Then the surface area \(S\) is \[ \begin{array}{rcl} S& =&\int\limits\int_{\kern-11ptR}\sqrt{\dfrac{a^{2}}{a^{2}-x^{2}-y^{2}}}\,d\!A \underset{\underset{{\color{#0066A7}{\hbox {a>0}}}}{\color{#0066A7}{\uparrow }}}{=} \int\limits\int_{\kern-11ptR}\dfrac{a}{\sqrt{a^{2}-r^{2}}} \,r\,dr\,d\theta \underset{\underset{{\color{#0066A7}{\hbox{Double the area}}}}{\color{#0066A7}{\uparrow}}}{=} 2\int_{0}^{\pi /2}\!\!\int_{0}^{a\cos \theta }\dfrac{a}{\sqrt{a^{2}-r^{2}}} \,r\,dr\,d\theta \notag \\ \quad \\ &=&-2a\int_{0}^{\pi /2}\Big[ \sqrt{a^{2}-r^{2}}\Big] _{0}^{a\cos \theta }d\theta =-2a\int_{0}^{\pi /2}(a\sin \theta -a)\,d\theta\\ &=&-2a^{2}\big[-\cos \theta -\theta \big] _{0}^{\pi /2}=a^{2}(\pi -2) \end{array} \]
NOW WORK
Problem 13.