Chapter 15

Printed Page AN-71

Section 15.1

1. Vector field

2. False

3. Vectors

4. True

5. The vector field is pictured below. See the Student Solutions Manual for a description.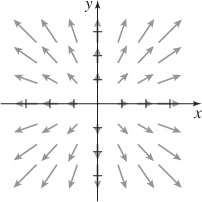

7. The vector field is pictured below. See the Student Solutions Manual for a description.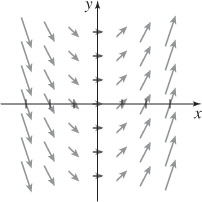

9. The vector field is pictured below. See the Student Solutions Manual for a description.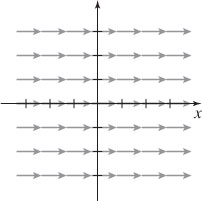

11. The vector field is pictured below. See the Student Solutions Manual for a description.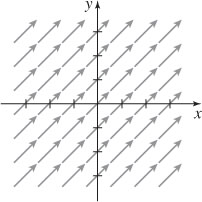

13. The vector field is pictured below. See the Student Solutions Manual for a description.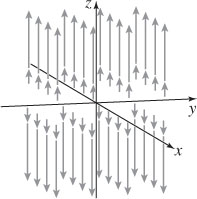

15. The vector field is pictured below. See the Student Solutions Manual for a description.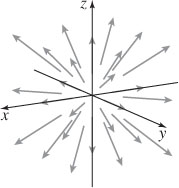

17. $\nabla f(x,y)=\sin y{\bf i}+(x \cos y - \sin y){\bf j}$

19. $\nabla f(x,y,z) = (2xy + y) {\bf i} + (x^2 + x + 2yz) {\bf j} + y^2 {\bf k}$

21. See Student Solutions Manual.

Section 15.2

1. True

2.

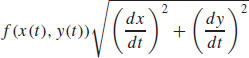
3. False

4.

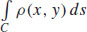
5. False

6. True

7.

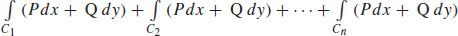
8. False

9.

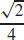
11.

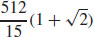
13.

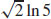
15.

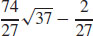
17. π

19. (a)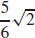

(b)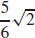

21. (a)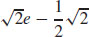

(b)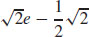

23.

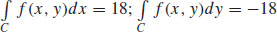
25.

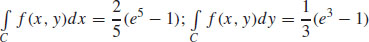
27. (a)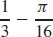

(b)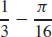

29. (a) 5

(b) 6.15

31. 3

33. 0

35.

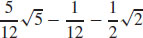
37.

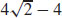
39.

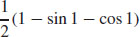
41. 1

43. −128

45. −128

47. 3

49.

51. 0

53.

55. π

57. 1

59.

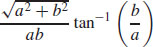
61.

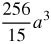
63. 2πa + a²π

65.

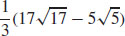
67.

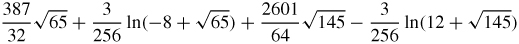
69.

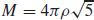
71.

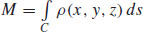
73. M = 20π + 40π²

75. See Student Solutions Manual.

77.

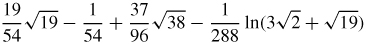
79. See Student Solutions Manual.

81. (a and b) See Student Solutions Manual.

Section 15.3

1. False

2. (d)

3. True

4. (c)

5. Closed

6. 0

7. False

8. True

9. False

10. True

11. False

12.

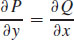
13. (a)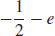

(b)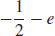

(c)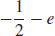

15. 8

17. 108

19. ln 13 − ln 5

21.

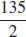
23.

25. 8

27. 0

29. 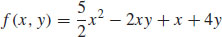+ K

31. f(x, y) = x ln y + x² + K

33. f is a conservative vector field.

35. f is a conservative vector field.

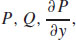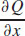37. (a) and are continuous everywhere in the xy-plane, and .

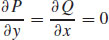(b) 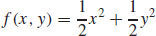+ K

(c)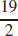

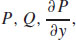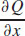39. (a) and are continuous everywhere in the xy-plane, and .

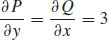(b) 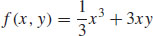+ K

(c)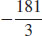

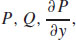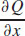41. (a) and are continuous everywhere in the xy-plane, and .

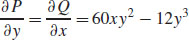(b) f (x, y) = x⁴ + 10x²y³ − 3xy⁴ + y⁵ + K

(c) 9

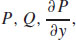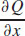43. (a) and are continuous everywhere in the xy-plane, and .

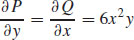(b) f(x, y) = x³y² + K

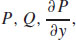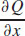45. (a) and are continuous everywhere in the xy-plane, and .

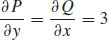(b) 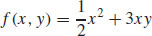+ K

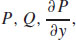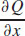47. (a) and are continuous everywhere in the xy-plane, and .

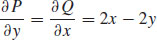(b) f(x, y) = x²y − xy² + K

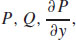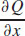49. (a) and are continuous everywhere in the xy-plane, and .

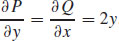(b) 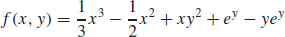+ K

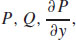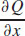51. (a) and are continuous everywhere in the xy-plane, and .

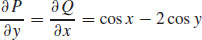(b) f(x, y) = y sin x − 2x sin y + K

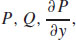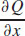53. (a) and are continuous everywhere in the xy-plane, and .

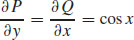(b) f(x, y) = x² + y sin x + K

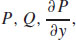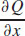55. and are continuous everywhere in the rectangle, and 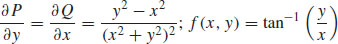+ K

57. (a) See Student Solutions Manual.

(b) 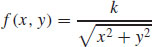+ K

59. See Student Solutions Manual.

Section 15.4

1. Energy

2. True

3. False

4. (d)

5. motion; position

6. False

7. 1

9.

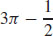
11.

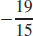
13.

15.

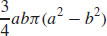
17. 0

19.

21. 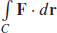along the first path is 0. 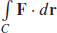along the second path is −1.

23.

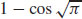
25. The work done is 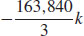, where k is a constant of proportionality.

27.

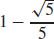
29.

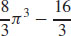
31. See Student Solutions Manual.

33. (a) See Student Solutions Manual.

(b) The escape speed for Earth is 11.2 kilometers per second.

(c) The escape speed for Mars is 5.0 kilometers per second.

(d) The escape speed for the sun is 617.6 kilometers per second.

Section 15.5

1. line; double

2.

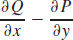
3. False

4. Area

5. −12

7. −12

9. 0

11.

13.

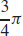
15. 0

17.

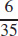
19.

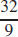
21. −2π

23. −2π

25.

27.

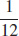
29. 2

31.

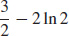
33. 3π

35. See Student Solutions Manual.

37.

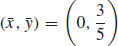
39.

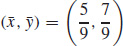
41. 0

43.

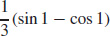
45. Answers will vary.

47. Answers will vary.

49. See Student Solutions Manual.

51. Any piecewise smooth, simple closed curve not passing through the origin and not containing the origin in its interior.

53. See Student Solutions Manual.

55. See Student Solutions Manual.

Section 15.6

1. (b)

2. (c)

3. (c)

4. (a)

5. (a) For u = 0: the line r(0,v) = −5v i+(1+v)k; for υ = 0: the line r (u,0) = ui+2u j+(1−u)k.

(b) x+2y+5z = 5

7. (a) For u = 0: the point (0, 0, 0); for υ = 0: the line r(u,0) = u i + uk.

(b) x² + y² = z², 0 ≤ z ≤ 2

9.

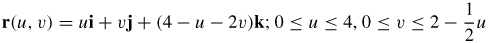
11. r (u, υ) ui + υ j +sin (u² υ)k; −1 ≤ u ≤ 2, u² ≤ υ ≤ u + 2

13. (a) 10x − 2y − 5z = 40

(b) r(t) = (7 + 10t) i + (5 − 2 t) j + (4 − 5t) k

15. (a)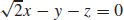

(b)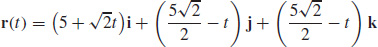

17.

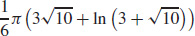
19.

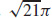
21. 16 π

23. (E)

25. (B)

27. (D)

29. r(u, υ) = 4 cos u i + 4 sin u j + υk; 0 ≤ u ≤ 2π, 0 ≤ υ ≤ 3

31. (a)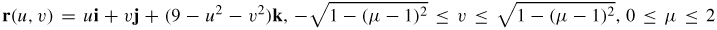

(b) ${{\bf r}}(r,\theta ) = r\cos \theta {{\bf i}} + r\sin \theta {{\bf j}} + (9- r^2) {{\bf k}}$; $0 \leq r \leq 2, -\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}$

33. (a)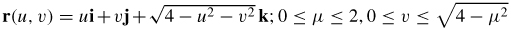

(b)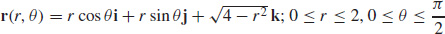

(c)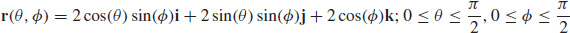

35. (a) z = 1

(b)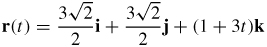

37.

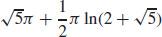
39. (a) r(θ, φ) = cos(θ) sin(φ)i + 3 sin(θ) sin(φ)j + 2 cos(φ)k; 0 ≤ θ ≤ 2π, 0 ≤ φ ≤ π

(b) See Student Solutions Manual.

(c) $S=\int_{0}^{2\pi}\int_{0}^{\pi}\sqrt{36\cos^{2} \theta \sin^{4} \phi + 4\sin^{2}\theta \sin^{4} \phi + 9\sin^{2} \phi \cos \phi\, d\phi d\theta }$

41. (a)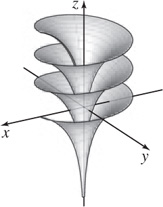

(b)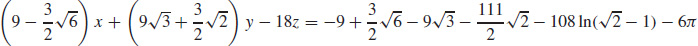

(c)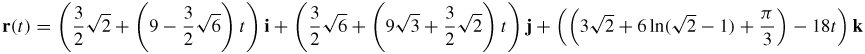

43. (a) r(u, υ) = (b + a cos u) cos υi + (b + a cos u) sin υj + a sin uk

(b)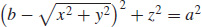

45. See Student Solutions Manual.

47.

(a) r(u, υ) = a cosh ui + (b sinh u cos υ)j + (c sinh u sin υ)k

(b)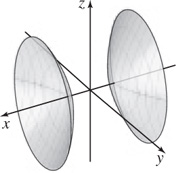

Section 15.7

1. (c)

2. (b)

3.

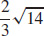
5.

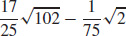
7.

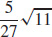
9. 0

11.

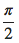
13.

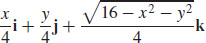
15.

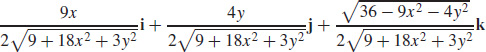
17.

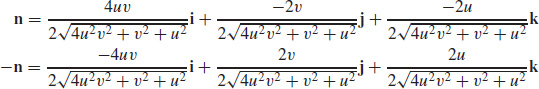
19. ρ

21. 0

23. 3ρ

25. 3ρ

27. 2π

29.

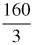
31. −5

33.

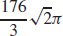
35.

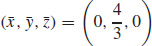
37.

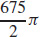
39.

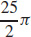
41. See Student Solutions Manual.

43.

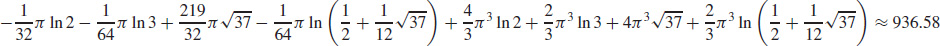
45. 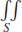F · ndS is equal to the surface area of S.

Section 15.8

1. False

2.

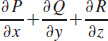
3. div F = 2x+2y+2z

5. div F = 4

7. div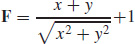

9.

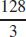
11. 3

13. 80π

15. 4π

17.

19. See Student Solutions Manual.

21.

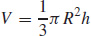
23. 4000π

25. See Student Solutions Manual.

27. See Student Solutions Manual.

29. 2π

31. See Student Solutions Manual.

33. See Student Solutions Manual.

Section 15.9

1. False

2. −xi − yj + (2z + 2)k

3. (c)

4. False

5. 2ω

6. False

7. curl F = 0

9. curl F = −xi + xyj + (z − xz)k

11. curl F = −y²cos zi + (6xyz − e^2z)j − 3xz²k

13. curl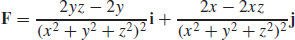

15. curl F = −ze^xz j

17. curl F = −i − j − k

19. 2π

21. −2π

23. π

25. 0

27. 0

29. 4π

31. curl F = 0. Force F is a conservative vector field.

33. curl F ≠ 0. Force F is not a conservative vector field.

35.

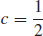
37. See Student Solutions Manual.

39. 0

41. curl F = −2 k. Answers for paths may vary.

43. See Student Solutions Manual.

45. Force F is a conservative vector field. The work done is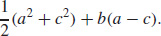

47. See Student Solutions Manual.

49. See Student Solutions Manual.

Review Exercises

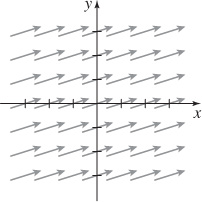
29.

3.

5. (a)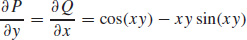

(b) sin 1

7. −2

9. (a) ∇ f (x, y) = F(x, y)

(b) 62

11.

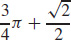
13.

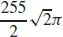
15.

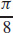
17. π

19. 108

21. −2

23. 12π

25. 7π

27. r(θ, z) = (5 cos θ)i + (2 sin θ)j + zk; 0 ≤ θ ≤ 2π, 1 ≤ z ≤ 6

29.

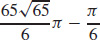
31.

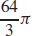
33. 0

35.

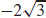
37. (a) div F = −z sin x + cos y

(b) curl F = (cos x − e^x)j

(c) 0

39. (a) div F = 3

(b) curl F = 0

(c) 0

41. 0

43.

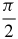
45.

47. F is not a conservative vector field because curl F ≠ 0.