15.6 Parametric SurfacesPrinted Page 1016
In Chapter P, we observed that the graph of an explicitly defined function y=f(x) satisfies the Vertical-line Test. We also saw that some graphs, such as circles, do not pass the Vertical-line Test. The equations of such graphs may be defined implicitly as F(x,y)=0. Then in Chapters 9 and 12, we found that parametric equations x=x(t) , y=y(t) and vector-valued functions r=r(t)=x(t)i+y(t)j, where a≤t≤b, allow us to represent a curve in a plane that is not necessarily the graph of function. Similarly, parametric equations x=x(t), y=y(t), z=z(t) and vector functions r=r(t)=x(t)i+y(t)j+z(t)k, where a≤t≤b, represent curves in space.
In this section, we define parametric equations and vector-valued functions that represent surfaces in space. Since a surface in space requires two independent variables, the parametric representation of a surface involves two parameters, u and v.
DEFINITION Parametric Surface
Suppose x=x(u,v)y=y(u,v)z=z(u,v)
are functions of two variables that are defined on a region R in the uv -plane. Also suppose that the functions are continuous and one-to-one* on the interior of R. Then u and v are parameters; x=x(u,v), y=y(u,v), z=z(u,v) are parametric equations; and the set of points defined by the parametric equations is a parametric surface.
The vector-valued function r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k
is called a parametrization of the surface. The region R is the parameter domain of r, and the range of r is the surface traced out by r.
Just as we can graph a function z=f(x,y) using contour lines or graph a quadric surface using traces, we can graph parametric surfaces using coordinate curves.
∗We require the parametrization to be one-to-one on the interior of R so that the surface does not fold over on itself.
1017
DEFINITION Coordinate Curves
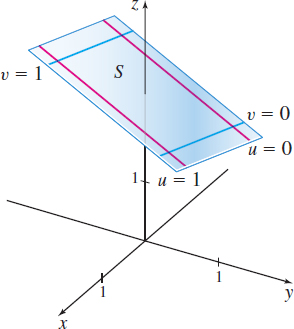
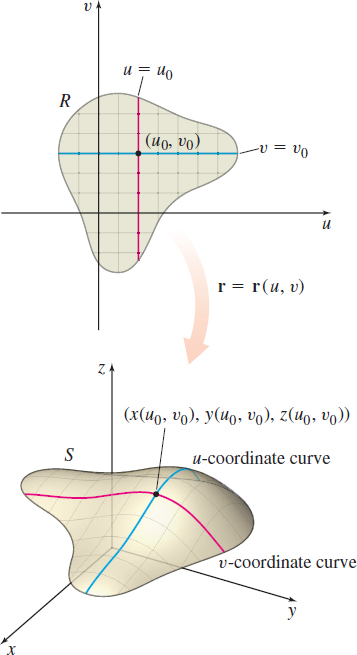
Suppose S is a surface with parametrization r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k and parameter domain R. Then the curve traced out by r=r(u,v) as (u,v) ranges over R, while holding v=v0 constant, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \mathbf{r}( u,v_{0}) =x\left( u,v_{0}\right) \mathbf{i}+y( u,v_{0}) \mathbf{j}+z( u,v_{0}) \mathbf{k} }}
is called a u-coordinate curve.
Similarly, the curve traced out as (u,v) ranges over R, while holding u=u_{0} constant, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \mathbf{r}( u_{0},v) =x( u_{0},v) \mathbf{i}+y( u_{0},v) \mathbf{j}+z( u_{0},v) \mathbf{k} }}
is called a v-coordinate curve.
Suppose the surface S is parametrized by \mathbf{r=r}(u,v) and parameter domain R. Then if we hold u=u_{0} constant in the uv -plane, we obtain the vertical line u=u_{0}. Similarly, if we hold v=v_{0} constant, we obtain a horizontal line v=v_{0}. The portions of these lines that are in the interior of the parameter domain R map to coordinate curves on the surface S. By sketching several coordinate curves, we obtain a wireframe plot of the surface S, as shown in Figure 40.
1 Describe Surfaces Defined ParametricallyPrinted Page 1017
EXAMPLE 1Describing a Parametric Surface
- (a) Describe the parametric surface S given by \mathbf{r}(u,v) =( 1+2u+v) \mathbf{i}+(u-v) \mathbf{j} +(3+v) \mathbf{k}.
- (b) Find a rectangular equation for S.
Solution (a) We begin by finding several coordinate curves. We choose to use v=0, v=1, u=0, and u=1, but any numbers will do.
When v=0, the u-coordinate curve is \mathbf{r} ( u,0) = (1+2u) \mathbf{i}+u\mathbf{j}+3\mathbf{k}.
When v=1, the u-coordinate curve is \mathbf{r} ( u,1) = (2+2u) \mathbf{i}+ ( u-1) \mathbf{j}+4\mathbf{k}.
When u=0, the v-coordinate curve is \mathbf{r} ( 0,v) = ( 1+v) \mathbf{i}-v\mathbf{j}+(3+v) \mathbf{k}.
When u=1, the v-coordinate curve is \mathbf{r} ( 1,v) =(3+v) \mathbf{i}+ ( 1-v) \mathbf{j}+(3+v) \mathbf{k}.
The graph of the parametric surface is a plane as shown in Figure 41.
(b) To find a rectangular equation for the surface, we write the components of \mathbf{r=r}(u,v) as a system of equations. Since \mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}=x(u,v) \mathbf{i}+y(u,v) \mathbf{j}+z(u,v) \mathbf{k}, we have \left\{ \begin{array}{ll@{\qquad}l} x=2u+v+1 & &{\color{#0066A7}{(1)}}\\ y=u-v & & {\color{#0066A7}{(2)}}\\ z= v+3 & & {\color{#0066A7}{(3)}} \end{array} \right.
If we eliminate u and v from this system, we will have an expression involving x, y, and z. We eliminate v by adding equations (1) and (2) and equations (2) and (3) . \begin{equation*} \begin{array}{ll@{\qquad\qquad}l} x+y=3u+1 & & \color{#0066A7}{{\hbox{(4) Add \(1\) and \(2\).}}}\\ y+z= \hspace{6pt}u+3 & &\color{#0066A7}{{\hbox{(5) Add \(2\) and \(3\).}}} \end{array} \end{equation*}
Now we eliminate u: \begin{equation*} \begin{array}{ll@{\qquad}l} \hspace{48pt}x+ y = 3u+1 & & \color{#0066A7}{(4)} \\[5pt] \hspace{27pt}\underline{\,\ -3y-3z=-3u-9} & \,\ \ \ \ \ \ \ \ \ \ & \color{#0066A7}{{\hbox{Multiply (5) by \(-3\).}}} \\ \hspace{21pt}x-2y-3z=-8 & & \color{#0066A7}{{\hbox{Add.}}} \end{array} \end{equation*}
This is the equation of a plane whose normal vector is \mathbf{i}-2\mathbf{j}-3\mathbf{k}.
1018
In Example 1, there were no restrictions on the parameters u and v, so the parametric surface S is the entire plane. By restricting the parameter domain, we can define a half-plane or a parallelogram. For some surfaces, such as the one in Example 2 , the parameter domain is restricted by the nature of the surface.
EXAMPLE 2Describing a Parametric Surface
Describe the parametric surface S parametrized by \begin{equation*} \mathbf{r}(u,v) =( 3+\cos v) \cos u\,\mathbf{i} +( 3+\cos v) \sin u\,\mathbf{j}+\sin v\mathbf{k} \end{equation*}
where 0\leq u\leq 2\pi and 0\leq v\leq 2\pi .
Solution We begin by finding some u-coordinate curves. Since the parametrization involves trigonometric functions, we choose 0,\dfrac{\pi }{2},\pi , and \dfrac{3\pi }{2}. Then the u-coordinate curves are \begin{equation*} \begin{array}{rcl@{\qquad}rrcl} \mathbf{r}(u,0) &=&4\cos u\,\mathbf{i}+4\sin u\,\mathbf{j} & \mathbf{r}\left( u,\dfrac{\pi }{2}\right) &=&3\cos u\,\mathbf{i}+3\sin u\,\mathbf{j+k}\\[5pt] \mathbf{r}( u,\pi ) &=&2\cos u\,\mathbf{i}+2\sin u\,\mathbf{j} & \mathbf{r}\left( u,\dfrac{3\pi }{2}\right) &=&3\cos u\,\mathbf{i}+3\sin u\,\mathbf{j-k} \end{array} \end{equation*}
We identify the graphs of each of these curves by using parametric equations. For example, for \mathbf{r}(u,0) , we have x=4\cos u, y=4\sin u, and x^{2}+y^{2}=( 4\cos u) ^{2}+( 4\sin u)^{2}=4^{2}( \cos ^{2}u+\sin ^{2}u) =4^{2}
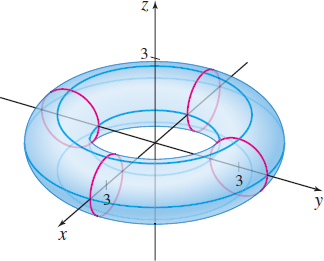
a circle of radius 4 centered at the origin. Similarly, \mathbf{r=r} ( u,\pi ) is a circle of radius 2 centered at the origin. The graphs of \mathbf{r}\left( u,\dfrac{\pi }{2}\right) and \mathbf{r}\left( u,\dfrac{3\pi }{2}\right) are both circles of radius 3, but the center of \mathbf{r=r}\left( u,\dfrac{\pi }{2}\right) is at ( 0,0,1) and the center of \mathbf{r=r}\left( u,\dfrac{3\pi }{2}\right) is at ( 0,0,-1) . Do you see why? See the blue circles in Figure 42.
Using 0,\dfrac{\pi }{2},\pi , and \dfrac{3\pi }{2} for u, we obtain the v-coordinate curves: \begin{array}{rcl@{\qquad}llcl} \mathbf{r}( 0,v) &=&( 3+\cos v) \mathbf{i}+\sin v\,\mathbf{k} & \mathbf{r}\left( \dfrac{\pi }{2},v\right) =( 3+\cos v) \,\mathbf{j}+\sin v\,\mathbf{k} \\[5pt] \mathbf{r}( \pi ,v) &=&-( 3+\cos v) \,\mathbf{i}+\sin v\, \mathbf{k} & \mathbf{r}\left( \dfrac{3\pi }{2},v\right) =-( 3+\cos v) \,\mathbf{j}+\sin v\,\mathbf{k} \end{array}
Again, we identify the graphs of these curves as circles. Each graph is a circle of radius 1, but the centers of the circles \mathbf{r=r}(0,v) , \mathbf{r=r}( \pi ,v) , \mathbf{r=r}\left( \dfrac{\pi }{2},v\right), and \mathbf{r=r}\left( \dfrac{3\pi }{2},v\right) are ( 3,0,0) , ( -3,0,0) , (0,3,0) , and ( 0,-3,0) , respectively. See the red circles in Figure 42.
The surface S is a torus. This particular torus results from revolving a circle of radius 1 about a circle of radius 3 centered at the origin.
NEED TO REVIEW?
A torus is discussed in Section 6.8, p. 464.
NOW WORK
2 Find a Parametric Representation of a SurfacePrinted Page 1018
NEED TO REVIEW?
Finding parametric representations of functions of one variable is discussed in Section 9.1, pp. 641-642.
Suppose we know the implicit equation F( x,y,z) =0 of a surface. If this equation can be solved explicitly for one of the variables, then the function has a natural parametrization. For example, if z=f(x,y) , then x=u, y=v, and z=f(u,v) parametrizes the surface. So, if a surface can be described by an equation explicitly solved for one coordinate in terms of the other two, we can use these two coordinates as parameters and obtain a parametrization.
1019
EXAMPLE 3Representing a Surface Parametrically
Find a parametrization of the surface S given by x+y^{2}+z=5\qquad 0\leq x\leq 1\qquad -1\leq y\leq 1
Solution We begin by expressing S as an explicit function of x and y. z=f(x,y) =5-x-y^{2}
Since z is a function of x and y, we let x=u and y=v. Then the parametric equations of S are x=u\qquad y=v\qquad z=5-u-v^{2}
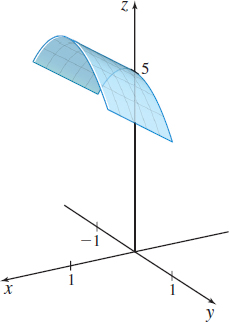
Using these parametric equations, we obtain \mathbf{r}(u,v) =u\mathbf{i}+v\mathbf{j}+( 5-u-v^{2}) \mathbf{k}\qquad 0\leq u\leq 1\qquad -1\leq v\leq 1
The graph of the surface \mathbf{r}(u,v) =u\mathbf{i}+v\mathbf{j}+( 5-u-v^{2}) \mathbf{k}, 0\leq u\leq 1 and -1\leq v\leq 1, is shown in Figure 43.
Alternatively, in Example 3, we could solve for x and get x=5-z-y^{2}. Then using u=y and v=z, we obtain \begin{equation*} \mathbf{r}(u,v) =( 5-v-u^{2}) \mathbf{i}+u\,\mathbf{ j}+v\,\mathbf{k} \end{equation*}
However, in this case, finding the bounds for u and v is not as straightforward. Setting x=0 and x=1 yields z=5-y^{2} and z=4-y^{2}, and so 4-u^{2}\leq v\leq 5-u^{2} and -1\leq u\leq 1.
NOW WORK
EXAMPLE 4Parametrizing a Sphere
Find a parametrization for a sphere S of radius 2 centered at the origin.
Solution The equation of the sphere, x^{2}+y^{2}+z^{2}=4, in rectangular coordinates cannot be expressed explicitly as a function of two of its variables. However, in spherical coordinates, the sphere has the explicit equation \rho =2. So if we use the spherical coordinates \theta and \phi as parameters, then parametric equations of the sphere are given by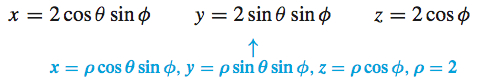
and a parametrization of S is \begin{equation*} \mathbf{r}\left( \theta ,\phi \right) =2\cos \theta \sin \phi \,\mathbf{i} +2\sin \theta \sin \phi \,\mathbf{j}+2\cos \phi \,\mathbf{k} \end{equation*}
where 0\leq \theta \leq 2\pi and 0\leq \phi \leq \pi .
NEED TO REVIEW?
Spherical coordinates are discussed in Section 14.8, pp. 956-959.
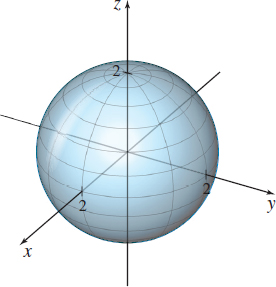
The sphere \rho =2 is shown in Figure 44. Notice the coordinate curves (latitude and longitude lines) on the sphere.
NOW WORK
Different parametrizations of the same surface each produce the same graph but may have different coordinate curves.
1020
EXAMPLE 5Parametrizing a Cone Using Different Coordinate Systems
Find a parametrization of the surface S defined by the cone z=\sqrt{3x^{2}+3y^{2}}\qquad x^{2}+y^{2}\leq 16
- (a) Using rectangular coordinates.
- (b) Using cylindrical coordinates.
- (c) Using spherical coordinates.
Solution (a) The equation is given in rectangular coordinates and is written explicitly as a function z=f(x,y) . So, we define x=u, y=v, z=\sqrt{3u^{2}+3v^{2}}. Then a parametrization of the cone is \mathbf{r}(u,v) =u\mathbf{i}+v\mathbf{j}+\sqrt{3u^{2}+3v^{2}}\, \mathbf{k}\qquad u^{2}+v^{2}\leq 16
NEED TO REVIEW?
Cylindrical coordinates are discussed in Section 14.7, pp. 950-954.
(b) In cylindrical coordinates, the cone is given by z=\sqrt{3x^{2}+3y^{2}}=\sqrt{3}\sqrt{( r\cos \theta ) ^{2}+(r\sin \theta ) ^{2}}=\sqrt{3}\sqrt{r^{2}}=\sqrt{3}\,r
where z is expressed explicitly in terms of r and \theta . So if we use r and \theta as parameters, then a parametrization of the cone is \begin{eqnarray*} \mathbf{r}( r,\theta ) =r\cos \theta \,\mathbf{i}+ \underset{\underset{\color{#0066A7}{x=r\cos \theta ,y= r\sin \theta , z=\sqrt{3}r}}{\color{#0066A7}{\uparrow}}}{r\sin \theta \, \mathbf{j}}+\sqrt{3}r\,\mathbf{k}\qquad 0\leq r\leq 4\quad 0\leq \theta \leq 2\pi \end{eqnarray*}
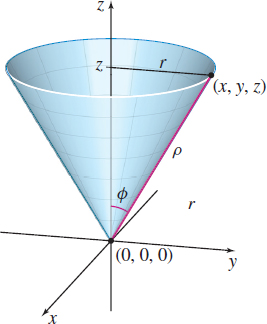
(c) In spherical coordinates, the equation of a half cone, where z\geq 0, is \phi =a, 0< a <\dfrac{\pi }{2}. We use Figure 45 to find a. \begin{eqnarray*} \tan \phi &=&\dfrac{r}{z}=\dfrac{r}{\sqrt{3}r}=\dfrac{1}{\sqrt{3}}\qquad \color{#0066A7}{{\hbox{\(z=\sqrt{3}r\)}}}\\[6pt] \phi &=&\tan ^{-1}\dfrac{1}{\sqrt{3}}=\dfrac{\pi }{6}=a \end{eqnarray*}
Using \rho and \theta as parameters, parametric equations for the cone in spherical coordinates are \begin{eqnarray*} x\underset{\underset{\color{#0066A7}{\sin \tfrac{\pi }{6}=\tfrac{1}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{ \rho }{2}\cos \theta \qquad y\underset{\underset{\color{#0066A7}{\sin \tfrac{\pi }{6}=\tfrac{1}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{\rho }{2}\sin \theta \qquad z \underset{\underset{\color{#0066A7}{\cos \tfrac{\pi }{6}=\tfrac{\sqrt{3}}{2}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{\sqrt{3}}{2}\rho \end{eqnarray*}
Now we find the parameter domain. Since z^{2}=3x^{2}+3y^{2} \ \hbox{and}\ \rho ^{2}=x^{2}+y^{2}+z^{2}=x^{2}+y^{2}+ (\underset{\color{#0066A7}{z^{2}}}{\underbrace{ 3x^{2}+3y^{2}}})=4x^{2}+4y^{2}
we have 0\leq \rho ^{2}=4(x^{2}+y^{2}) \leq 4\,{\cdot}\, 16=64,\ \hbox{or equivalently,}\ 0\leq \rho \leq 8.
The parameter domain of the cone is 0\leq \rho \,\leq 8 and 0\leq \theta \leq 2\pi . Then a parametrization of the cone is \mathbf{r}( \rho ,\theta ) =\dfrac{\rho }{2}\cos \theta \,\mathbf{ i}+\dfrac{\rho }{2}\sin \theta \,\mathbf{j}+\dfrac{\sqrt{3}}{2}\rho \, \mathbf{k}\qquad 0\leq \rho \leq 8\quad 0\leq \theta \leq 2\pi
1021
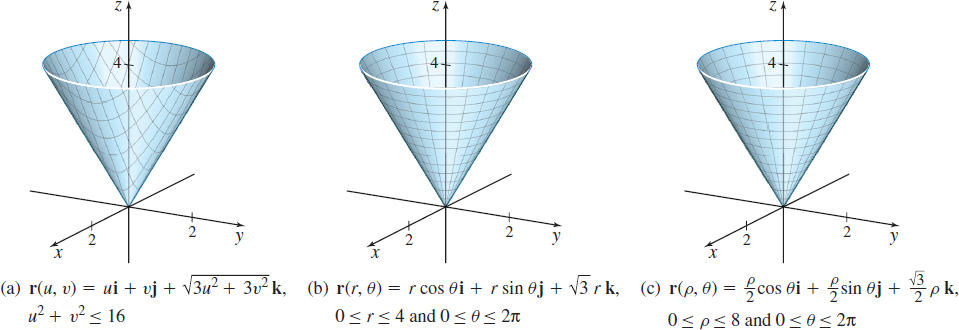
The graphs of the three parametrizations of the cone z=\sqrt{3x^{2}+3y^{2}}, x^{2}+y^{2}\leq 16 are shown in Figure 46.
Notice that although the three graphs are identical, the parametrizations are not. The cylindrical and spherical parametrizations are different, but both result in coordinate curves that are rays and circles. The rectangular parametrization results in coordinate curves that are hyperbolas. Notice also that the parameter domains of the cylindrical and spherical parametrizations are rectangular regions, but the parameter domain of the rectangular parametrization is a disk. Because of this, the cylindrical and spherical parametrizations are easier to work with.
NOW WORK
Now that we have seen how to parametrize a surface S, we return to a basic problem of calculus—the tangent problem. If a surface S is parametrized by the vector function \mathbf{r}=\mathbf{r}(u,v) , consider the tangent plane to S at a point P_{0}=\mathbf{r}(u_{0},v_{0}) on the surface.
The coordinate curves \mathbf{r=r}\left( u,v_{0}\right) and \mathbf{r=r}\left( u_{0},v\right) both lie on the surface S and intersect at the point P_{0}=\mathbf{r}( u_{0},v_{0}) . Then the partial derivative \mathbf{r}_{u}(u_{0},v_{0}) =\dfrac{\partial }{\partial u} x(u_{0},v_{0}) \mathbf{i}+\dfrac{\partial }{\partial u}y(u_{0},v_{0}) \mathbf{j}+\dfrac{\partial }{\partial u}z(u_{0},v_{0}) \mathbf{k}
provided it exists, is a tangent vector to the u-coordinate curve at P_{0}.
Similarly, the partial derivative \mathbf{r}_{v}(u_{0},v_{0}) =\dfrac{\partial }{\partial v} x(u_{0},v_{0}) \mathbf{i}+\dfrac{\partial }{\partial v}y(u_{0},v_{0}) \mathbf{j}+\dfrac{\partial }{\partial v}z(u_{0},v_{0}) \mathbf{k}
NEED TO REVIEW?
Tangent vectors to a curve are discussed in Section 11.2, pp. 767-769.
provided it exists, is a tangent vector to the v-coordinate curve at P_{0} .
To obtain a formula for the tangent plane to a surface S, we require \mathbf{r}=\mathbf{r}(u,v) to have certain properties.
DEFINITION Smooth Parametrization
A parametrization \mathbf{r}=\mathbf{r}(u,v) is called a smooth parametrization if
- \mathbf{r} is continuous and has continuous partial derivatives in the parameter domain R, and
- \mathbf{r}_{u}\times \mathbf{r}_{v}\neq \mathbf{0} in R.
A surface S that can be given a smooth parametrization is called a smooth surface.
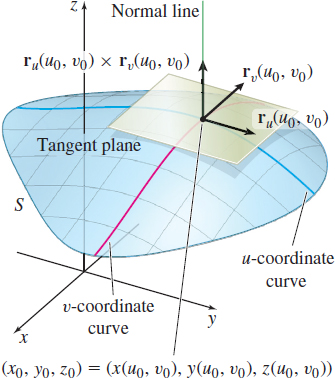
A smooth surface has a tangent plane at every point. If S is a smooth surface, then the tangent plane to S at a point P_{0}=\mathbf{r}(u_{0},v_{0}) is the plane containing the tangent vectors \mathbf{r}_{u}(u_{0},v_{0}) and \mathbf{r}_{v}(u_{0},v_{0}) . Also, the vector \mathbf{r}_{u}\times \mathbf{r}_{v} is normal to the tangent plane. See Figure 47.
3 Find Equations for a Tangent Plane and a Normal LinePrinted Page 1022
1022
EXAMPLE 6Find Equations for a Tangent Plane and a Normal Line
- (a) Find an equation of the tangent plane to the surface S parametrized by \mathbf{r=r}(u,v) =3u\mathbf{i}+( 6-u^{2}-v^{2}) \mathbf{j}+2v \mathbf{k\ } at the point ( -3,1,4) .
- (b) Find an equation of the normal line to the tangent plane at (-3,1,4) .
Solution (1) We begin by finding the values of the parameters at the point ( -3,1,4) . That is, we solve the system of equations \left\{ \begin{array}{rcl@{\qquad}r} 3u &=&-3 & \color{#0066A7}{{\hbox{\((1)\)}}}\\ 6-u^{2}-v^{2}&=& 1 & \color{#0066A7}{{\hbox{\((2)\)}}}\\ 2v&=& 4 & \color{#0066A7}{{\hbox{\((3)\)}}} \end{array} \right.
From ( 1) we find u=-1, and from (3) we find v=2. [Checking, we find these values also satisfy (2).]
We now find the tangent vectors \mathbf{r}_{u} and \mathbf{r}_{v}. \begin{array}{@{\hspace*{-2.2pc}}rcl@{\qquad}lrll} \mathbf{r}_{u} &=&\dfrac{\partial }{\partial u}( 3u) \mathbf{i}+ \dfrac{\partial }{\partial u}( 6-u^{2}-v^{2}) \mathbf{j}+\dfrac{ \partial }{\partial u}\left( 2v\right) \mathbf{k}=3\mathbf{i}-2u\,\mathbf{j} & \mathbf{r}_{u}( -1,2) &=&3\mathbf{i}+2\,\mathbf{j}\\[4pt] \mathbf{r}_{v} &=&\dfrac{\partial }{\partial v}( 3u) \mathbf{i}+ \dfrac{\partial }{\partial v}( 6-u^{2}-v^{2}) \mathbf{j}+\dfrac{ \partial }{\partial v}( 2v) \mathbf{k}=-2v\mathbf{j}+2\,\mathbf{k} & \mathbf{r}_{v}( -1,2) &=&-4\mathbf{j}+2\, \mathbf{k} \end{array}
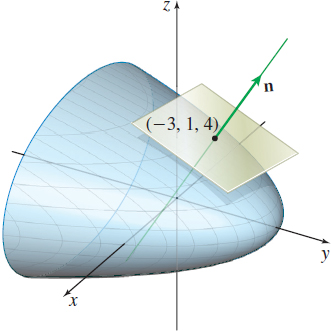
The normal vector \mathbf{n} to the tangent plane at ( -3,1,4) is \mathbf{n} = \mathbf{r}_u ( -1,2) \times \mathbf{r}_v ( -1,2) =\left\vert \begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] 3 & 2 & 0 \\[3pt] 0 & -4 & 2 \end{array} \right\vert =4\mathbf{i}-6\mathbf{j}-12\mathbf{k}
An equation of the tangent plane is 4( x+3) -6( y-1) -12( z-4) =0\qquad\hbox{or equivalently}\qquad 4x-6y-12z=-66
(b) The normal line to the tangent plane contains the point ( -3,1,4) and is parallel to the vector \mathbf{n}=4\mathbf{i}-6\mathbf{j} -12\mathbf{k}. A parametrization of the normal line is \mathbf{r}(t) = ( -3+4t ) \mathbf{i}+ ( 1-6t ) \mathbf{j} + ( 4-12t ) \mathbf{k}
See Figure 48.
NOW WORK
EXAMPLE 7Finding a Tangent Plane and a Normal Line
A surface S is defined by x^{2}+z^{2}=25 and 0\leq y\leq 10.
- (a) Find a smooth parametrization for S.
- (b) Find an equation of the tangent plane to S at the point ( -3,5,4) .
- (c) Find an equation of the normal line to the tangent plane at (-3,5,4) .
Solution (a) Since S is a circular cylinder, we choose a parametrization that uses a variation of cylindrical coordinates. If x=r\cos \theta , y=y, and z=r\sin \theta , then x^{2}+z^{2}=r^{2}=25, or equivalently, r=5. Then parametric equations for the cylinder are x=5\cos \theta \qquad y=y\qquad z=5\sin \theta
and a parametrization of S is \begin{equation*} \mathbf{r}( \theta ,y) =5\cos \theta\ \mathbf{i}+y\mathbf{j}+5\sin \theta\ \mathbf{k} \end{equation*}
where the parameter domain is 0\leq \theta \leq 2\pi and 0\leq y\leq 10.
1023
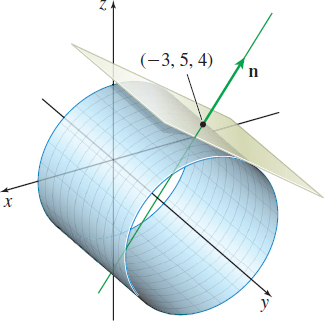
To determine whether this is a smooth parametrization, we find the partial derivatives of \mathbf{r=\mathbf{r}}( \theta ,y). \mathbf{r}_{\theta }( \theta ,y) =-5\sin \theta\ \mathbf{i}+5\cos \theta\ \mathbf{k}\qquad \mathbf{r}_{y}( \theta ,y) =\mathbf{j}
Each of these is continuous. Now \mathbf{r}_{\theta }\times \mathbf{r}_{y}= \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ -5\sin \theta & 0 & 5\cos \theta \\ 0 & 1 & 0 \end{array}\right| =-5\cos \theta\ \mathbf{i}-5\sin \theta\ \mathbf{k}
Since \left\Vert \mathbf{r}_{\theta }\times \mathbf{r}_{y}\right\Vert =\left\Vert -5\cos \theta\ \mathbf{i}-5\sin \theta\ \mathbf{k}\right\Vert =\sqrt{25\cos ^{2}\theta +25\sin ^{2}\theta }=5, then \mathbf{r}_{\theta }\times \mathbf{r}_{y}\neq \mathbf{0}. So, \mathbf{r}=\mathbf{r}( \theta ,y) \mathbf{\ } is a smooth parametrization, and S is a smooth surface.
(b) At the point ( -3,5,4) , we have 5\cos \theta =-3, y=5, and 5\sin \theta =4. Then the normal vector \mathbf{n} to the plane at ( -3,5,4) is \mathbf{r}_{\theta }\times \mathbf{r} _{y}=-5\left( -\dfrac{3}{5}\right) \mathbf{i}-5\left( \dfrac{4}{5}\right) \mathbf{k}=3\mathbf{i}-4\mathbf{k}. An equation of the tangent plane is 3( x+3) -4( z-4) =0\qquad \hbox{or equivalently}\qquad 3x-4z=-25
(c) The normal line to the tangent plane contains the point ( -3,5,4) and is parallel to 3\mathbf{i}-4\mathbf{k}. A parametrization of the normal line is \ \mathbf{r}(t) =(-3+3t) \mathbf{i}+5\mathbf{j}+( 4-4t) \mathbf{k}. See Figure 49.
4 Find the Surface Area of a Parametrized SurfacePrinted Page 1023
NOTE
Whenever a surface S has a smooth parametrization, we can find its surface area using a double integral.
In Section 14.5, we developed the formula S=\iint\limits_{\kern-3ptR}\sqrt{[f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}\, dA
for the surface area of a function z=f(x,y)\geq 0 defined on a closed, bounded region R. Here, we investigate how to find the surface area of more general parametric surfaces.
Suppose the smooth surface S has the parametrization \begin{equation*} \mathbf{r}(u,v) =x(u,v) \mathbf{i}+y(u,v) \mathbf{j}+z(u,v) \mathbf{k} \end{equation*}
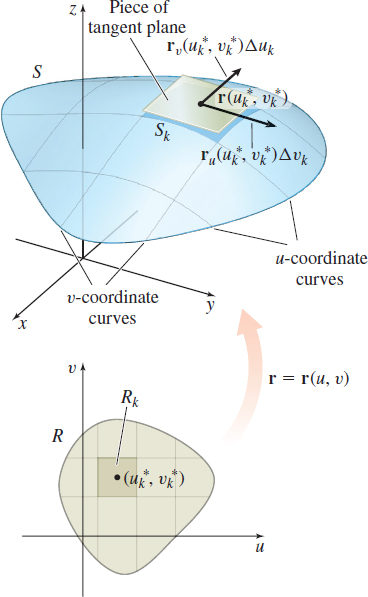
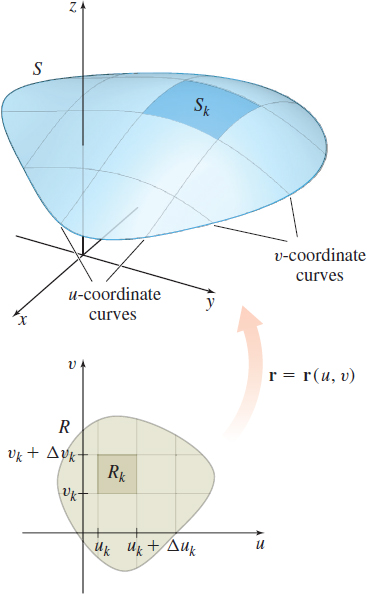
and its parameter domain R is a closed, bounded region of the uv-plane. Then following our usual practice, we partition the region R into subrectangles using lines parallel to the u-axis and the v-axis and discarding any subrectangles not lying entirely in R. Suppose we are left with n subrectangles R_{k}, k=1,2,\ldots ,n, with width \Delta u_{k} and height \Delta v_{k}. The area of the subrectangle R_{k} is \Delta A_{k}=\Delta u_{k}\Delta v_{k}.
The kth subrectangle R_{k} is formed by the lines u=u_{k}, u=u_{k}+\Delta u_k, v=v_{k}, and v=v_{k}+\Delta v_{k}. We define the norm \Vert P\Vert as the length of the largest diagonal of the subrectangles. The portions of the lines forming the edges of the subrectangle R_{k} map to portions of their corresponding coordinate curves on the surface S. That is, each subrectangle R_{k} maps into a closed, curved patch S_{k} on S. See Figure 50.
We now choose a point \big(u_{k}^{\ast },v_{k}^{\ast }\big) in each subrectangle. In a small enough region, a smooth surface can be approximated by its tangent planes. So, the area of S_{k} can be approximated using part of the tangent plane at \mathbf{r=r}\big( u_{k}^{\ast },v_{k}^{\ast }\big) , or more specifically, S_{k} can be approximated by the parallelogram formed by the vectors \mathbf{r}_{u}\big( u_{k}^{\ast },v_{k}^{\ast }\big) \Delta u_{k} and \mathbf{r}_{v}\big( u_{k}^{\ast },v_{k}^{\ast }\big) \Delta v_{k} (tangents to the coordinate curves). See Figure 51. The area of this parallelogram is \Delta S_{k}=\left\Vert \mathbf{r}_{u}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\times \mathbf{r}_{v}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\right\Vert \,\Delta A_{k}=\left\Vert \mathbf{r}_{u}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\times \mathbf{r} _{v}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\right\Vert \,\Delta u_{k}\,\Delta v_{k}
Then the surface area differential dS is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dS=\left\Vert \mathbf{r}_{u}(u,v)\times \mathbf{r}_{v}(u,v)\right\Vert dA=\left\Vert \mathbf{r}_{u}(u,v)\times \mathbf{r}_{v}(u,v)\right\Vert du\,dv }}
1024
Since for each k, \Delta S_{k} approximates the surface area of S_{k}, then the sum \begin{equation*} \sum\limits_{k=1}^{n}\Delta S_{k}=\sum\limits_{k=1}^{n}\left\Vert \mathbf{r}_{u}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\times \mathbf{r}_{v}\big(u_{k}^{\ast },v_{k}^{\ast }\big)\right\Vert \,\Delta u_{k}\,\Delta v_{k} \end{equation*}
approximates the surface area of S. Since \mathbf{r}=\mathbf{r}(u,v) is a smooth parametrization, \lim\limits_{\left\Vert P\right\Vert \rightarrow 0}\sum\limits_{k=1}^{n}\Delta S_{k} exists and equals the surface area of S. \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \hbox{Surface area of } S=\iint\limits_{\kern-3ptR}dS=\iint\limits_{\kern-3ptR}\left\Vert \mathbf{r}_{u}\times \mathbf{r}_{v}\right\Vert \,du\,dv }} \tag{1}
In the special case that S is the graph of a function z=f(x,y) and we use the parametrization, x=x, y=y, and z=f(x,y) , we obtain \begin{equation*} dS=\sqrt{[ f_{x}(x,y) ] ^{2}+[ f_{y}(x,y) ] ^{2}+1}\,dx\,dy \end{equation*}
and the formula for surface area \begin{equation*} S=\iint\limits_{\kern-3ptR}\sqrt{[f_{x}(x,y)]^{2}+[f_{y}(x,y)]^{2}+1}\, dx\,dy \end{equation*}
from Section 14.5.
EXAMPLE 8Finding the Surface Area of a Torus
Find the surface area of the torus parametrized by \begin{equation*} \mathbf{r}(u,v) =( 3+\cos v) \cos u\,\mathbf{i} +( 3+\cos v) \sin u\,\mathbf{j}+\sin v\mathbf{k} \end{equation*}
where 0\leq u\leq 2\pi and 0\leq v\leq 2\pi .
Solution This is the torus graphed in Figure 42. To use formula (1) to find the area of a parametrized surface, we need to find the partial derivatives of \mathbf{r=r}(u,v) . \begin{eqnarray*} \mathbf{r}_{u}(u,v) &=&( 3+\cos v) \left( -\sin u\right) \,\mathbf{i}+( 3+\cos v) \cos u\,\mathbf{j} \\[4pt] \mathbf{r}_{v}(u,v) &=& (-\sin v) \cos u \mathbf{i} -\sin v\sin u\,\mathbf{j}+\cos v\mathbf{k} \end{eqnarray*}
Next we find the cross product: \begin{eqnarray*} \mathbf{r}_{u}\times \mathbf{r}_{v} &=& \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -( 3+\cos v) \sin u & ( 3+\cos v) \cos u & 0 \\[3pt] -\sin v\cos u & -\sin v\sin u & \cos v \end{array}\right|\\[5pt] &=&( 3+\cos v) \left( \cos u\cos v\mathbf{i}+\sin u\cos v\mathbf{j }+\sin v\mathbf{k}\right) \end{eqnarray*}
Then \begin{eqnarray*} \hspace{-2pc}\left\Vert \mathbf{r}_{u}\times \mathbf{r}_{v}\right\Vert &=&\sqrt{( 3+\cos v) ^{2}( \cos ^{2}u\cos ^{2}v+\sin ^{2}u\cos ^{2}v+\sin ^{2}v) } \\ &=&( 3+\cos v) \sqrt{\cos ^{2}v( \cos ^{2}u+\sin ^{2}u) +\sin ^{2}v}=( 3+\cos v) \sqrt{\cos ^{2}v+\sin ^{2}v}\\ &=&3+\cos v \end{eqnarray*}
Now using formula (1), the surface area of S is \begin{eqnarray*} \iint\limits_{\kern-3ptR}( 3+\cos v)\, du\,dv&=&\int_{0}^{2\pi }\int_{0}^{2\pi }( 3+\cos v)\, dv\,du=\int_{0}^{2\pi }\big[ 3v+\sin v \big] _{0}^{2\pi }du\\[4pt] &=&\int_{0}^{2\pi }6\pi du=12\pi ^{2} \end{eqnarray*}