2.5 The Derivative of the Trigonometric FunctionsPrinted Page 185
OBJECTIVES
When you finish this section, you should be able to:
1 Differentiate Trigonometric FunctionsPrinted Page 185
NEED TO REVIEW?
The trigonometric functions are discussed in Section P.6, pp. 49-56.
To find the derivatives of y=sinx and y=cosx, we use the limits lim
that were established in Section 1.4.
186
THEOREM Derivative of y = sin x
The derivative of y = sin x is y^\prime =\cos x. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt] {y^\prime = \dfrac{d}{dx}\sin x=\cos x}}
NEED TO REVIEW?
Basic trigonometric identities are discussed in Appendix A.4, pp. A-32 to A-35.
Proof
\begin{array}{lcll} y^\prime &=&\lim\limits_{h\rightarrow 0}\dfrac{\sin(x+h) -\sin x }{h} & {\color{#0066A7}{\hbox{The definition of a derivative.}}} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\sin x\cos h+\sin h\cos x-\sin x}{h} & {\color{#0066A7}{\hbox{\(\sin (A+B) =\sin A\,\cos B+\sin B\,\cos A.\)}}} \\ &=&\lim\limits_{h\rightarrow 0}\left[ \dfrac{\sin x\cos h-\sin x}{h}+\dfrac{\sin h\cos x}{h}\right] & {\color{#0066A7}{\hbox{Rearrange terms.}}} \\ &=&\lim\limits_{h\rightarrow 0}\left[ \sin x\cdot \dfrac{\cos h-1}{h}+\dfrac{\sin h}{h}\cdot \cos x\right] & {\color{#0066A7}{\hbox{Factor.}}} \\ &=&\left[\lim\limits_{h\rightarrow 0}\sin x\right]\! \left[\lim\limits_{h\rightarrow 0} \dfrac{\cos h-1}{h}\right] +\left[\lim\limits_{h\rightarrow 0}\cos x\right]\!\left[ \lim\limits_{h\rightarrow 0}\dfrac{\sin h}{h}\right] & {\color{#0066A7}{\hbox{Use properties of limits.}}}\\ &=&\sin x\cdot 0+\cos x\cdot 1=\cos x & {\color{#0066A7}{\hbox{\(\lim\limits_{\theta \rightarrow 0}\dfrac{\cos \theta -1}{\theta } =0 ; \quad \lim\limits_{\theta \rightarrow 0}\dfrac{\sin \theta}{\theta } =1.\)}}} \end{array}
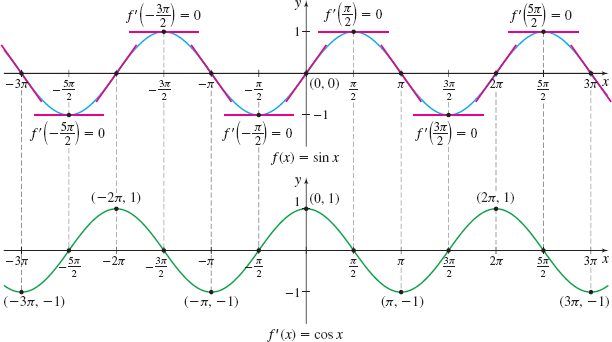
The geometry of the derivative \dfrac{d}{dx}\sin x=\cos x is shown in Figure 26. On the graph of f(x) =\sin x, the horizontal tangents are marked as well as the tangent lines that have slopes of 1 and −1. The derivative function is plotted on the second graph and those points are connected with a smooth curve.
EXAMPLE 1Differentiating the Sine Function
Find y^\prime if:
- (a) y=x+4\sin x
- (b) y=x^{2}\sin x
- (c) y=\dfrac{\sin x}{x}
- (d) y=e^{x}\sin x
Solution
- (a) y^\prime =\dfrac{d}{dx}(x+4\sin x) = \dfrac{d}{dx}x+\dfrac{d}{dx}(4 \sin x) = 1+4 \dfrac{d}{dx} \sin x = 1 + 4 \cos x
- (b) y^\prime = \dfrac{d}{dx}(x^{2} \sin x) = x^{2} \left[\dfrac{d}{dx} \sin x\right] +\left[\dfrac{d}{dx}x^{2}\right] \sin x = x^{2}\cos x+2x\sin x
187
- (c) y^\prime =\dfrac{d}{dx}\left(\dfrac{\sin x}{x}\right) = \dfrac{\left[\dfrac{d}{dx}\sin x\right] \cdot x-\sin x\cdot \left[ \dfrac{d }{dx}x\right]}{x^{2}}=\dfrac{x\cos x-\sin x}{x^{2}}
- (d) \begin{eqnarray*} y^\prime &=& \dfrac{d}{dx}(e^{x}\sin x) = (e^{x} \dfrac{d}{dx}\sin x + \left(\dfrac{d}{dx}e^{x}\right) \sin x = e^{x}\cos x+e^{x}\sin x\\ &=& e^{x} (\cos x+\sin x) \end{eqnarray*}
NOW WORK
THEOREM Derivative of y= cos x
The derivative of y= \cos x is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\cos x=-\sin x }
You are asked to prove this in Problem 75.
EXAMPLE 2Differentiating Trigonometric Functions
Find the derivative of each function:
- (a) f(x) =x^{2}\cos x
- (b) g(\theta ) =\dfrac{\cos \theta }{1-\sin \theta }
- (c) F(t) =\dfrac{e^{t}}{\cos t}
Solution
- (a) \begin{eqnarray*} f^\prime (x) &=& \frac{d}{dx} (x^{2}\cos x) = x^{2}\frac{d}{dx}\cos x + (\frac{d}{dx} x^{2}) (\cos x)\\ &=& x^{2}(-\sin x) + 2x\cos x = 2x\cos x - x^{2}\sin x \end{eqnarray*}
- (b) \begin{eqnarray*} g^\prime (\theta) &=& \frac{d}{d\theta} (\frac{\cos\theta}{1-\sin\theta}) = \frac{(\frac{d}{d\theta}\cos\theta) (1-\sin\theta) -(\cos\theta) [\frac{d}{d\theta}(1-\sin\theta) ]}{(1-\sin\theta)^{2}}\\ &=& \frac{-\sin\theta (1-\sin\theta) -\cos\theta (-\cos\theta)}{(1-\sin\theta)^{2}} =\frac{-\sin\theta +\sin^{2}\theta +\cos^{2}\theta}{(1-\sin\theta)^{2}}\\ &=&\frac{-\sin\theta+1}{(1-\sin\theta)^{2}}=\frac{1}{1-\sin\theta} \end{eqnarray*}
- (c) \begin{eqnarray*} F\prime(t) &=&\frac{d}{dt}(\frac{e^{t}}{\cos t}) = \frac{(\frac{d}{dt}e^{t}) (\cos t) -e^{t}(\frac{d}{dt}\cos t)}{\cos^{2}t}=\frac{e^{t}\cos t-e^{t}(-\sin t) }{\cos ^{2}t}\\ &=&\frac{e^{t}(\cos t+\sin t)}{\cos^{2}t} \end{eqnarray*}
NOW WORK
EXAMPLE 3Identifying Horizontal Tangent Lines
Find all points on the graph of f(x) =x+\sin x where the tangent line is horizontal.
Solution Since tangent lines are horizontal at points on the graph of f where f^\prime (x) =0, we begin by finding f^\prime: f^\prime (x) =1+\cos x Now we solve the equation f^\prime (x) =0. \begin{array}{rcl@{\qquad}l} f^\prime (x) &=& 1+\cos x=0 \\[0pt] \cos x &=& -1 \\[0pt] x &=& (2k+1) \pi &\hbox{where }{k}\hbox{ is an integer} \end{array}
188
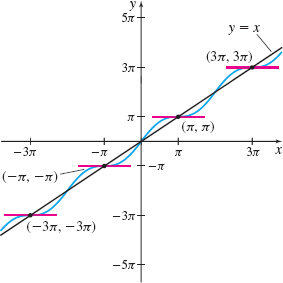
The graph of f( x) =x+\sin x has a horizontal tangent line at each of the points ( ( 2k+1) \pi , ( 2k+1) \pi ), k an integer. See Figure 27 for the graph of f with the horizontal tangent lines marked. Notice that each of the points with a horizontal tangent line lies on the line y=x.
NOW WORK
The derivatives of the remaining four trigonometric functions are obtained using trigonometric identities and basic derivative rules. We establish the formula for the derivative of y=\tan x in Example 4. You are asked to prove formulas for the derivative of the secant function, the cosecant function, and the cotangent function in the exercises. (See Problems 76–78.)
EXAMPLE 4Differentiating y= tanx
Show that the derivative of y = tan x is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\tan x=\sec ^{2}x}
Solution \begin{eqnarray*} y^\prime &=&\dfrac{d}{dx}\tan x\underset{\underset{\color{#0066A7}{\hbox{Identity}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{d}{dx}\dfrac{\sin x}{\cos x}\underset{\underset{\color{#0066A7}{\hbox{Quotient Rule}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{\left[ \dfrac{d}{dx}\sin x\right] \cos x-\sin x\left[ \dfrac{d}{dx}\cos x\right] }{\cos ^{2}x} \\ &=&\dfrac{\cos x\cdot \cos x-\sin x\cdot (-\sin x)}{\cos ^{2}x}=\dfrac{\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}=\dfrac{1}{\cos ^{2}x}=\sec ^{2}x \end{eqnarray*}
NOW WORK
Table 4 lists the derivatives of the six trigonometric functions along with the domain of each derivative.
| Derivative Function | Domain of the Derivative Function |
|---|---|
| \dfrac{d}{dx}\sin x=\cos x | ( -\infty ,\infty ) |
| \dfrac{d}{dx}\cos x=-\sin x | ( -\infty ,\infty ) |
| \dfrac{d}{dx}\tan x=\sec ^{2}x | \left\{ x|x\neq \dfrac{2k+1}{2}\pi, k\hbox{ an integer}\right\} |
| \dfrac{d}{dx}\cot x=-\csc ^{2}x | \{ x|x\neq k\pi, k \hbox{ an integer}\} |
| \dfrac{d}{dx}\csc x=-\csc x\cot x | \{ x|x\neq k\pi, k\hbox{ an integer}\} |
| \dfrac{d}{dx}\sec x=\sec x\tan x | \left\{ x|x\neq \dfrac{2k+1}{2}\pi, k\hbox{ an integer}\right\} |
189
EXAMPLE 5Evaluating the Second Derivative of a Trigonometric Function
Find f'' \left( \dfrac{\pi }{4}\right) if f( x) =\sec x.
NOTE
If the trigonometric function begins with the letter c, that is, cosine, cotangent, or cosecant, then its derivative has a minus sign.
Solution If f( x) =\sec x, then f^\prime (x) =\sec x\tan x and \begin{eqnarray*} f'' ( x) &=&\dfrac{d}{dx}( \sec x\tan x) \underset{\underset{\color{#0066A7}{\hbox{Use the Product Rule.}}}{{{\color{#0066A7}\uparrow }}}}= \sec x\!\left( \dfrac{d}{dx}\tan x\right) +\left( \dfrac{d}{dx}\sec x\right) \tan x \\ \\ &=&\sec x\cdot \sec ^{2}x+( \sec x\tan x) \tan x=\sec ^{3}x+\sec x\tan ^{2}x \end{eqnarray*}
Now, \begin{eqnarray*} f'' \left( \dfrac{\pi }{4}\right) =\sec ^{3}\!\left( \dfrac{\pi }{4} \right) +\sec\! \left( \dfrac{\pi }{4}\right) \tan ^{2}\!\left( \dfrac{\pi }{4} \right) \underset{\underset{\color{#0066A7}{\hbox{sec} \dfrac{\pi }{4}=\sqrt{2};\hbox{ tan}\dfrac{\pi }{4}=1}} {{{\color{#0066A7}\uparrow }}}}= ( \sqrt{2}) ^{3}+\sqrt{2}\cdot 1^{2}=2 \sqrt{2}+\sqrt{2}=3\sqrt{2} \\ \end{eqnarray*}
NOW WORK
Simple harmonic motion is a repetitive motion that can be modeled by a trigonometric function. A swinging pendulum and an oscillating spring are examples of simple harmonic motion.
EXAMPLE 6Analyzing Simple Harmonic Motion
An object hangs on a spring, making it 2 m long in its equilibrium position. See Figure 28. If the object is pulled down 1 m and released, it will oscillate up and down. The length l of the spring after t seconds is modeled by the function l( t) =2+\cos t.
- (a) How does the length of the spring vary?
- (b) Find the velocity of the object.
- (c) At what position is the speed of the object a maximum?
- (d) Find the acceleration of the object.
- (e) At what position is the acceleration equal to 0?
Solution
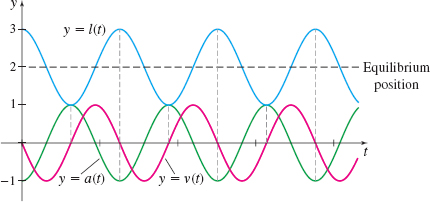
- (a) Since l(t) =2+\cos t and -1 ≤ \cos t ≤ 1, the length of the spring oscillates between 1 m and 3 m.
- (b) The velocity v of the object is v=l' ( t) =\dfrac{d}{dt}\left( 2+\cos t\right) =-\sin t
- (c) Speed is the magnitude of velocity. Since v=-\sin t, the speed of the object is \left\vert v\right\vert =\left\vert -\sin t\right\vert =\left\vert \sin t\right\vert. Since -1 ≤ \sin t ≤ 1, the object moves the fastest when \left\vert v\right\vert =\left\vert \sin t\right\vert =1. This occurs when \sin t=\pm 1 or, equivalently, when \cos t=0. So, the speed is a maximum when l( t) =2, that is, when the spring is at the equilibrium position.
- (d) The acceleration a of the object is given by a=l'' ( t) =\dfrac{d}{dt}l' (t)=\dfrac{d}{dt} ( -\sin t) =-\cos t
- (e) Since a=-\cos t, the acceleration is zero when \cos t=0. This occurs when l( t) =2, that is, when the spring is at the equilibrium position. At this time, the speed is maximum.
190
Figure 29 shows the graphs of the length of the spring y=l( t), the velocity y=v( t), and the acceleration y=a( t).