5.2 The Definite IntegralPrinted Page 353
353

OBJECTIVES
When you finish this section, you should be able to:
The area A under the graph of y=f(x) from a to b is obtained by finding A=lim
where the following assumptions are made:
ORIGINS
Riemann sums are named after the German mathematician Georg Friedrich Bernhard Riemann (1826–1866). Early in his life, Riemann was home schooled. At age 14, he was sent to a lyceum (high school) and then the University of Göttingen to study theology. Once at Göttingen, he asked for and received permission from his father to study mathematics. He completed his PhD under Karl Friedrich Gauss (1777–1855). In his thesis, Riemann used topology to analyze complex functions. Later he developed a theory of geometry to describe real space. His ideas were far ahead of their time and were not truly appreciated until they provided the mathematical framework for Einstein's Theory of Relativity.
- The function f is continuous on [a,b].
- The function f is nonnegative on [a,b].
- The closed interval [a,b] is partitioned into n subintervals, each of length \Delta x=\dfrac{b - a}{n}
- f(c_{i}) is the absolute minimum value of f on the ith subinterval, i= 1,2,\ldots, n.
- f(C_{i}) is the absolute maximum value of f on the ith subinterval, i= 1,2,\ldots, n.
In Section 5.1, we found the area A under the graph of f from a to b by choosing either the number c_{i}, where f has an absolute minimum on the ith subinterval, or the number C_{i}, where f has an absolute maximum on the ith subinterval. Suppose we arbitrarily choose a number u_{i} in each subinterval [x_{i-1},x_i], and draw rectangles of height f(u_{i}) and width \Delta x. Then from the definitions of absolute minimum value and absolute maximum value f(c_{i}) \leq f (u_{i}) \leq f(C_{i})
and, since \Delta x > 0, f(c_{i}) \Delta x\leq f (u_{i}) \Delta x\leq f(C_{i}) \Delta x
Then \begin{eqnarray*} \sum\limits_{i=1}^{n}f (c_{i}) \Delta x & \leq &\sum\limits_{i=1}^{n}f (u_{i}) \Delta x\leq \sum\limits_{i=1}^{n}f (C_{i}) \Delta x \\ s_{n} &\leq &\sum\limits_{i=1}^{n}f(u_{i}) \Delta x\leq S_{n} \end{eqnarray*}
NEED TO REVIEW?
The Squeeze Theorem is discussed in Section 1.4, pp. 106-107.
Since \lim\limits_{n\rightarrow \infty }s_{n}=\lim\limits_{n\rightarrow \infty }S_{n}=A, by the Squeeze Theorem, we have \lim\limits_{n\rightarrow \infty }\sum\limits_{i=1}^{n}f (u_{i}) \Delta x=A
In other words, we can use any number u_{i} in the ith subinterval to find the area A.
1 Define a Definite Integral as the Limit of Riemann SumsPrinted Page 353
We now investigate sums of the form \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{i=1}^{n}f (u_{i}) \Delta x_{i}}}
using the following more general assumptions:
- The function f is not necessarily continuous on [a, b].
- The function f is not necessarily nonnegative on [a, b].
- The lengths \Delta x_{i}= x_{i}-x_{i-1} of the subintervals [x_{i-1},x_{i}] , i=1,2,\ldots ,n of [a,b] are not necessarily equal.
- The number u_{i} may be any number in the subinterval [x_{i-1}, x_{i}], i=1,2,\ldots ,n.
354
The sums {\sum\limits_{i=1}^{n}{f (u_{i}) }}\Delta x_{i}, called Riemann sums for f on [a, b], form the foundation of integral calculus.
EXAMPLE 1Forming Riemann Sums
For the function f(x) =x^{2}-3, 0\leq x\leq 6, partition the interval [0,6] into 4 subintervals [0,1], [1,2], [2,4], [4,6] and form the Riemann sum for which
- (a) u_{i} is the left endpoint of each subinterval.
- (b) u_{i} is the midpoint of each subinterval.
Solution In forming Riemann sums \sum\limits_{i=1}^{n}f(u_{i}) \Delta x_{i}, n is the number of subintervals in the partition, f(u_{i}) is the value of f at the number u_{i} chosen in the ith subinterval, and \Delta x_{i} is the length of the ith subinterval.
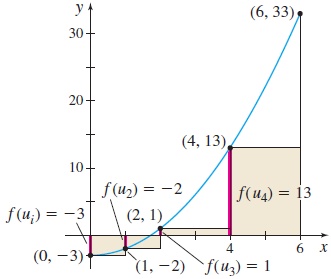
(a) Figure 16 shows the graph of f, the partition of the interval [0,6] into the 4 subintervals, and values of f(u_{i}) at the left endpoint of each subinterval, namely, \begin{array}{rcl@{\qquad}crcl} f(u_{1}) &=& f(0) =-3 & f(u_{2}) &=&f(1) =-2\\ f(u_{3}) &=& f(2) =1 & f(u_{4}) &=& f(4) = 13 \end{array}
The 4 subintervals have length \Delta x_{1}=1-0=1 \qquad \Delta x_{2}=2-1=1 \qquad \Delta x_{3}=4-2=2 \qquad \Delta x_{4}=6-4=2
The Riemann sum is formed by adding the products f(u_{i}) \Delta x_{i} for i=1,2,3,4. \sum\limits_{i=1}^{4} f(u_{i}) \Delta x_{i}=-3\cdot 1 + (-2) \cdot 1+1\cdot 2 + 13 \cdot 2=23
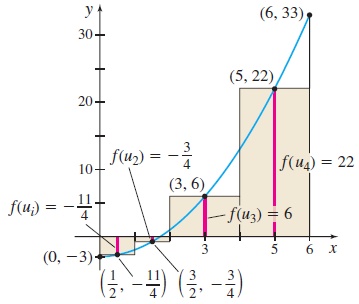
(b) See Figure 17. If u_{i} is chosen as the midpoint of each subinterval, then the value of f(u_{i}) at the midpoint of each subinterval is \begin{array}{rcl@{\qquad}crcl} f(u_{1}) &=& f\left(\dfrac{1}{2}\right) =-\dfrac{11}{4} & f(u_{2}) &=&f\left( \dfrac{3}{2}\right) =-\dfrac{3}{4}\\ f(u_{3}) &=&f (3) =6 & f(u_{4}) &=& f(5) = 22 \end{array}
The Riemann sum formed by adding the products f(u_{i}) \Delta x_{i} for i=1,2,3,4 is \sum\limits_{i=1}^{4}f(u_{i}) \Delta x_{i}=-\dfrac{11}{4} \cdot 1 + \left(-\dfrac{3}{4}\right) \cdot 1 + 6 \cdot 2 + 22 \cdot 2 =\dfrac{105}{2}=52.5
NOW WORK
Suppose a function f is defined on a closed interval [a,b], and we partition the interval [a,b] into n subintervals \lbrack x_{0}, x_{1}], \lbrack x_{1}, x_{2}], \lbrack x_{2}, x_{3}], \ldots , [x_{i-1},x_{i}], \ldots , \lbrack x_{n-1}, x_{n}]
where a=x_{0}\lt x_{1}\lt x_{2}\lt\cdots \lt x_{i-1} \lt x_{i}\lt\cdots \lt x_{n-1}\lt x_{n}=b
These subintervals are not necessarily of the same length. Denote the length of the first interval by \Delta x_{1}=x_{1}-x_{0}, the length of the second interval by \Delta x_{2}=x_{2}-x_{1}, and so on. In general, the length of the ith subinterval is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta x_{i}=x_{i}-x_{i-1}}}
355
for i=1, 2, \ldots , n. This set of subintervals of the interval [a,b] is called a partition of [a,b]. The length of the largest subinterval in a partition is called the norm of the partition and is denoted by \max \Delta x_{i}.
DEFINITION Definite Integral
Let f be a function defined on the closed interval [a,b]. Partition [a,b] into n subintervals of length \Delta x_{i}\,{=}\,x_{i}\,{-}\,x_{i-1}, i\,{=}\,1,2, \ldots , n. Choose a number u_{i} in each subinterval, evaluate f(u_{i}) , and form the Riemann sums {\sum\limits_{i=1}^{n}} {{f(u_{i})}}\Delta x_{i}. If \lim\limits_{{\max \Delta x}_{i} \rightarrow 0}{\sum\limits_{i=1}^{n}} {{f(u_{i})}}\Delta x_{i}=I exists and does not depend on the choice of the partition or on the choice of u_{i}, then the number I is called the Riemann integral or definite integral of f from a to b and is denoted by the symbol \int_{a}^{b} f (x)\,dx. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{a}^{b} f (x) dx=\lim\limits_{\max \Delta x_{i}\rightarrow 0} {\sum\limits_{i=1}^{n}} f(u_{i}) \Delta x_{i}}}
When the above limit exists, then we say that f is integrable over [a,b].
For the definite integral {\int_{a}^{b}{f(x)\,dx}}, the number a is called the lower limit of integration, the number b is called the upper limit of integration, the symbol \int (an elongated S to remind you of summation) is called the integral sign, f(x) is called the integrand, and dx is the differential of the independent variable x. The variable used in the definite integral is an artificial or a dummy variable because it may be replaced by any other symbol. For example, \int_{a}^{b} {f(x)\,dx} \qquad \int_{a}^{b} {f(t)\,dt} \qquad \int_{a}^{b}{f(s)\,ds}\qquad \int_{a}^{b} {f(\theta)\,d\theta}
all denote the definite integral of f from a to b, and if any of them exist, they are all equal to the same number.
EXAMPLE 2Expressing the Limit of Riemann Sums as a Definite Integral
- (a) Find the Riemann sums for f(x) =x^{2}-3 on the closed interval [0,6] for a partition of [0,6] into n subintervals of length \Delta x_{i}=x_{i}-x_{i-1}, i=1,2, \ldots , n.
- (b) Assuming that the limit of the Riemann sums exists as \max \Delta x_{i}\rightarrow 0, express the limit as a definite integral.
Solution (a) The Riemann sums for f(x)=x^{2}-3on the closed interval [0,6] are \sum\limits_{i=1}^{n}f(u_{i}) \Delta x_{i}=\sum\limits_{i=1}^{n}\big( u_{i}^{2}-3\big) \Delta x_{i}
where [0,6] is partitioned into n subintervals [x_{i-1}, x_{i}] , and u_{i} is some number in the subinterval [x_{i-1}, x_{i}], i=1,2, \ldots, n.
(b) Since \lim\limits_{\max \Delta x_{i}\rightarrow 0}\sum\limits_{i=1}^{n}\big( u_{i}^{2}-3\big) \Delta x_{i} exists, then \lim\limits_{\max \Delta x_i \rightarrow 0}\sum\limits_{i=1}^{n}\big(u_{i}^{2}-3\big) \Delta x_{i}=\int_{0}^{6}( x^{2}-3) dx
NOW WORK
356
If f is integrable over [a,b], then \lim\limits_{{\max \Delta x}_{i} \rightarrow 0}{\sum\limits_{i=1}^{n}} f (u_{i}) \Delta x_{i} exists for any choice of u_{i} in the ith subinterval, so we are free to choose the u_{i} any way we please. The choices could be the left endpoint of each subinterval, or the right endpoint, or the midpoint, or any other number in each subinterval. Also, \lim\limits_{{\max \Delta x}_{i} \rightarrow 0}{\sum\limits_{i=1}^{n}} f(u_{i})\Delta x_{i} is independent of the partition of the closed interval [a,b], provided {\max \Delta x}_{i} can be made as close as we please to 0. It is these flexibilities that make the definite integral so important in engineering, physics, chemistry, geometry, and economics.
In defining the definite integral {\int_{a}^{b} {f(x)\,dx,}} we assumed that a\lt b. To remove this restriction, we give the following definitions.
DEFINITION
- If f(a) is defined, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{a}^{a}f (x)\,dx=0 } }
- If a > b and if \int_{b}^{a}f (x)\,dx exists, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{a}^{b}f (x) dx=-\int_{b}^{a}f (x) dx } }
IN WORDS
Interchanging the limits of integration reverses the sign of the definite integral.
For example, \int_{1}^{1} x^{2}\,dx=0 \qquad \text{ and }\qquad \int_{3}^{2} x^{2}\,dx=-\int_{2}^{3} x^{2}\,dx
Next we give a condition on the function f that guarantees f is integrable. The proof of this result may be found in advanced calculus texts.
IN WORDS
If a function f is continuous on [a,b], then it is integrable over [a,b]. But if f is not continuous on [a,b], then f may or may not be integrable over [a,b].
THEOREM Existence of the Definite Integral
If a function f is continuous on a closed interval [a,b], then the definite integral \int_{a}^{b}f(x)\,dx exists.
The two conditions of the theorem deserve special attention. First, f is defined on a closed interval, and second, f is continuous on that interval. There are some functions that are continuous on an open interval (or even a half-open interval) for which the integral does not exist. For example, although f(x)=\dfrac{1}{x^{2}} is continuous on (0,1) (and on (0,1]), the definite integral {\int_{0}^{1}}\dfrac{{1}}{x^{2}} dx does not exist. Also, there are many examples of discontinuous functions for which the integral exists. (See Problems 64 and 65.)
2 Find a Definite Integral Using the Limit of Riemann SumsPrinted Page 356
Suppose f is integrable over the closed interval [a,b]. To find \int\nolimits_{a}^{b}f(x)\, dx=\lim\limits_{\max\Delta x_{i}\rightarrow 0}\ \sum\limits_{i=1}^{n} f(u_{i})\Delta x_{i}
using Riemann sums, we usually partition [a,b] into n subintervals, each of the same length \Delta x=\dfrac{b-a}{n}. Such a partition is called a regular partition. For a regular partition, the norm of the partition is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {\max \Delta x}_{i}={\dfrac{b-a}{n}}} }
357
Since \lim\limits_{n\rightarrow \infty }\dfrac{b-a}{n}=0, it follows that for a regular partition, the two statements {\max \Delta x}_{i} {\rightarrow 0}\qquad \text{ and }\qquad {n\rightarrow \infty }
are interchangeable. As a result, for regular partitions \Delta x= \dfrac{b-a}{n}, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{a}^{b}{f(x)\,dx=}\lim\limits_{{\max \Delta x}_{i} \rightarrow 0}{\sum\limits_{i=1}^{n}} {f(u_{i})} \Delta x_i=\lim\limits_{n\rightarrow \infty}{\sum\limits_{i=1}^{n}} {f(u_{i})}\Delta x } }
The next result uses Riemann sums to establish a formula to find the definite integral of a constant function.
THEOREM
If f(x) =h, where h is some constant, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[5pt]{ \int_{a}^{b}f(x)\,dx=\int_{a}^{b}h\,dx=h(b-a)} }
Proof
The constant function f(x) =h is continuous on the set of real numbers and so is integrable. We form the Riemann sums for f on the closed interval [a,b] using a regular partition. Then \Delta x_{i}=\Delta x=\dfrac{b-a}{n}, i=1,2, \ldots , n. The Riemann sums of f on the interval [a,b] are \begin{eqnarray*} \sum\limits_{i=1}^{n}f(u_{i}) \Delta x_{i} &=& \sum\limits_{i=1}^{n}f(u_{i}) \Delta x \underset{\underset{\color{#0066A7}{\hbox{\(f(x) =h\)}}}{\color{#0066A7}{\uparrow }}} {=} \sum\limits_{i=1}^{n}h\,\Delta x=\sum\limits_{i=1}^{n}h\left( \dfrac{b-a}{n}\right) \\ & =& h\left(\dfrac{b-a}{n}\right) \sum\limits_{i=1}^{n}1=h\left( \dfrac{b-a}{n}\right) \cdot n=h(b-a) \end{eqnarray*}
Then \lim\limits_{n\rightarrow \infty }\sum\limits_{i=1}^{n}f(u_{i}) \Delta x=\lim\limits_{n\rightarrow \infty} [h(b-a)] =h(b-a)
So, \int_{a}^{b}h\,dx=h(b-a)
For example, \begin{eqnarray*} \begin{array}{@{\hspace*{-4pc}}l} \int_{1}^{2}3\,dx=3(2-1) =3 \qquad \int_{2}^{6}dx=1(6-2) =4 \qquad \int_{-3}^{4} (-2)\, dx=(-2) [4- (-3 )] =-14 \end{array} \end{eqnarray*}
NOW WORK
EXAMPLE 3Finding a Definite Integral Using the Limit of Riemann Sums
Find {\int_{0}^{3}{(3x -8)}}\,dx.
Solution Since the integrand f(x) = 3x - 8 is continuous on the closed interval [0, 3], the function f is integrable over [0, 3]. Although we can use any partition of [0,3] whose norm can be made as close to 0 as we please, and we can choose any u_{i} in each subinterval, we use a regular partition and choose u_{i} as the right endpoint of each subinterval. This will result in a simple expression for the Riemann sums.
358
We partition [0,3] into n subintervals, each of length \Delta x=\dfrac{3-0}{n}=\dfrac{3}{n}. The endpoints of each subinterval of the partition, written in terms of n, are \begin{eqnarray*} x_{0}&=&0,\ x_{1}=\dfrac{3}{n},\ {x_{2}=2}\left({\dfrac{3}{n}}\right), \ldots , x_{i-1}=(i-1) \left(\dfrac{3}{n}\right),\\ x_{i} &=& i\left(\dfrac{3}{n}\right) , \ldots , x_{n}=n\left(\dfrac{3}{n}\right)=3 \end{eqnarray*}
The Riemann sums of f(x)=3x - 8 from 0 to 3, using u_{i}= x_{i}= \dfrac{3i}{n} (the right endpoint) and \Delta x=\dfrac{3}{n}, are 357 \begin{eqnarray*} \sum\limits_{i=1}^{n}\,f(u_{i})\,\Delta x_{i} &=&\sum\limits_{i=1}^{n}\,f(x_{i})\,\Delta x \underset{\underset{{\color{#0066A7}{\hbox{\(\Delta x=\dfrac{3}{n}\)}}}}{\color{#0066A7}{\left\uparrow\right.}}} {=} \sum\limits_{i=1}^{n}(3x_{i}-8)\dfrac{3}{n} \underset{\underset{{\color{#0066A7}{\hbox{\(x_{i}=\dfrac{3i}{n}\)}}}}{\color{#0066A7}{\left\uparrow\right.}}} {=} \sum\limits_{i=1}^{n}\left[ 3\left( {\dfrac{{3i}}{{n}}}\right) -8\right] \dfrac{3}{n} \\ &=& \sum \limits_{i=1}^{n}\left( \dfrac{27i}{n^{2}}-\dfrac{24}{n}\right) =\dfrac{27}{n^{2}}\sum\limits_{i=1}^{n}{i}-\dfrac{24}{n} \sum\limits_{i=1}^{n}1\\[5pt] &=&\dfrac{27}{n^{2}}\cdot \dfrac{n(n+1)}{{2}}-\dfrac{24}{{n} }\cdot n=\dfrac{27}{2}+\dfrac{27}{2n}-24 =-\dfrac{21}{2}+\dfrac{27}{2n} \end{eqnarray*}
Now {\int_{0}^{3}{(3x-8)\,dx=}}\lim\limits_{n\rightarrow \infty }\left( -\dfrac{21}{2}+\dfrac{27}{2n}\right) =-\dfrac{21}{2}
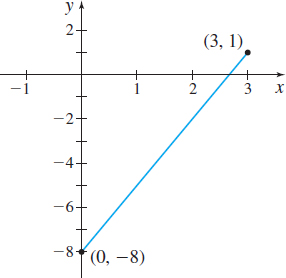
NOW WORK
Figure 18 shows the graph of f(x)=3x - 8 on [0,3] . Since f is not nonnegative on [0,3] , we cannot interpret {\int_{0}^{3}{(3x - 8)\,dx}} as an area. The fact that the answer is negative is further evidence that this is not an area problem. When finding a definite integral, do not presume it represents area. As you will see in Section 5.4 and in Chapter 6, the definite integral has many interpretations. Interestingly enough, definite integrals are used to find the volume of a solid of revolution, the length of a graph, the work done by a variable force, and other quantities.
EXAMPLE 4Interpreting a Definite Integral
Determine if each definite integral can be interpreted as an area. If it can, describe the area; if it cannot, explain why.
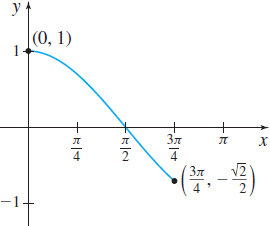
- (a) \int_{0}^{3\pi /4}\cos x\,dx
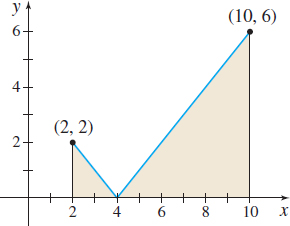
- (b) \int_{2}^{10}\left \vert x-4\right\vert dx
Solution (a) See Figure 19. Since \cos x\lt0 on the interval \left(\dfrac{\pi }{2},\dfrac{3\pi}{4}\right], the integral \int_{0}^{3\pi /4}\cos x\,dx cannot be interpreted as area.
(b) See Figure 20. Since \vert x-4\vert \geq 0 on the interval [2,10] , the integral \int_{2}^{10}\vert x-4\vert \,dx can be interpreted as the area enclosed by the graph of y=\vert x-4\vert , the x-axis, and the lines x=2 and x=10.
359
NOW WORK
EXAMPLE 5Finding a Definite Integral Using Technology
- (a)
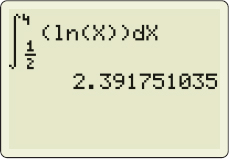
 Use a graphing utility to find \int_{1/2}^{4}\ln x\,dx
Use a graphing utility to find \int_{1/2}^{4}\ln x\,dx - (b)
 Use a computer algebra system to find \int_{1/2}^{4}\ln x\,dx.
Use a computer algebra system to find \int_{1/2}^{4}\ln x\,dx.
Solution (a) A graphing utility, such as a TI-84, provides only an approximate numerical answer to the integral \int_{1/2}^{4}\ln x\,dx. As shown in Figure 21, \int_{1/2}^{4}\ln\, x\,dx\approx 2.391751035.
(b) Because a computer algebra system manipulates symbolically, it can find an exact value of the definite integral. Using MuPAD in Scientific WorkPlace, we get \int_{1/2}^{4}\ln x\,dx= \dfrac{17}{2}\ln 2-\dfrac{7}{2}
An approximate numerical value of the definite integral using MuPAD is 2.3918.