8.9 Taylor Series; Maclaurin SeriesPrinted Page 611
We saw in Section 8.8 that it is often possible to obtain a power series representation for a function by starting with a known series and differentiating, integrating, or substituting.
612
But what if you have no initial series? In other words, so far we have seen that functions can be represented by power series, and if we know the sum of the power series, then we know the function. In this section, we investigate what the power series representation of a function must look like if it has a power series representation.
Consider the power series in (x−c): ∞∑k=0ak(x−c)k=a0+a1(x−c)+a2(x−c)2+⋯+an(x−c)n+⋯
and suppose its interval of convergence is the open interval (c−R,c+R), R>0. We define the function f as the series f(x)=∞∑k=0ak(x−c)k=a0+a1(x−c)+a2(x−c)2+⋯+an(x−c)n+⋯
The coefficients a0,a1,… can be expressed in terms of f and its derivatives in the following way. Repeatedly differentiate the function using the differentiation property of a power series, f′(x)=∞∑k=1kak(x−c)k−1=a1+2a2(x−c)+3a3(x−c)2+4a4(x−c)3+⋯f′′(x)=∞∑k=2[k(k−1)]ak(x−c)k−2=(2⋅1)a2+(3⋅2)a3(x−c)+(4⋅3)a4(x−c)2+⋯f′′′(x)=∞∑k=3[k(k−1)(k−2)]ak(x−c)k−3=(3⋅2⋅1)a3+(4⋅3⋅2)a4(x−c)+⋯
and for any positive integer n, f(n)(x)=∞∑k=nk(k−1)(k−2)⋯(k−n+1)ak(x−c)k−n=[n⋅(n−1)⋅…⋅1]an+[(n+1)⋅n⋅(n−1)⋅…⋅2]an+1(x−c)+⋯=n!an+(n+1)!an+1(x−c)+⋯
Now we let x=c in each derivative and solve for ak. f(c)=a0a0=f(c)f′(c)=a1a1=f′(c)f′′(c)=2a2a2=f′′(c)2!f′′′(c)=3!a3a3=f′′′(c)3!⋮⋮f(n)(c)=n!anan=f(n)(c)n!
If we substitute for ak in (1), we obtain f(x)=f(c)+f′(c)(x−c)+f′′(c)2!(x−c)2+⋯+f(n)(c)n!(x−c)n+⋯
ORIGINS
Colin Maclaurin (1698–1746) was a Scottish mathematician. An orphan, he and his brother were raised by an uncle. Maclaurin was 11 years old when he entered the University of Glasgow, and within a year he had taught himself Euclid’s elements (geometry). Maclaurin was 19 when he was appointed professor of Mathematics at the University of Aberdeen, Scotland. Maclaurin was an avid supporter of Newton’s mathematics. In response to a claim that Newton’s calculus lacked rigor, Maclaurin wrote the first systematic treatise on Newton’s methods. In it he used Taylor series centered about 0, which are now known as Maclaurin series.

and have proved the following result.
613
THEOREM Taylor Series; Maclaurin Series
Suppose f is a function that has derivatives of all orders on the open interval (c−R,c+R), R>0. If f can be represented by the power series ∞∑k=0ak(x−c)k, whose radius of convergence is R, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,4pt]{ \begin{array}{@{\hskip0pc}rcl} f(x)&=&f(c)+f^{\prime} (c)(x-c)+\frac{f^{\prime \prime} (c) }{2!}(x-c) ^{2}+\cdots +\frac{f^{(n) }(c)\,}{n!}(x-c)^{n}+\cdots \\[11pt] &=&\sum\limits_{k\,=\,0}^{\infty }\frac{f^{(k) }(c) }{k!}(x-c) ^{k} \hspace{120pt} (2)\\ \\ \end{array}}}
for all numbers x in the open interval (c-R,\,c+R). A power series that has the form of equation (2) is called a Taylor series of the function f.
When c=0, the Taylor series representation of a function f \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ f(x)=f(0)+f^{\prime} (0)\,x+\frac{f^{\prime \prime}(0) }{2!}x^{2}+\cdots +\frac{f^{(n)}(0)}{n!}x^{n}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\frac{f^{(k) }(0) }{k!}x^{k} }}
is called a Maclaurin series.
The Taylor series in (x-c) of a function f is referred to as the Taylor expansion of f about c; the Maclaurin series of a function f is called the Maclaurin expansion of f about 0.
In a Taylor series, all the derivatives are evaluated at c, and the interval of convergence has its center at c. In a Maclaurin series, all the derivatives are evaluated at 0, and the interval of convergence has its center at 0.
1 Express a Function as a Taylor Series or a Maclaurin SeriesPrinted Page 613
The next example shows what a Maclaurin expansion of f(x) =e^{x} must look like (if there is one).
EXAMPLE 1Expressing a Function as a Maclaurin Series
Assuming that f(x)=e^{x} can be represented by a power series in x, find its Maclaurin series.
Solution To express a function f as a Maclaurin series, we begin by evaluating f and its derivatives at 0. \begin{array}{rl@{\qquad}rll} f(x) & =e^{x} & f(0) &=1 \\ f^{\prime} (x)& =e^{x} & f^{\prime} (0) & =1 \\ f^{\prime \prime} (x) & =e^{x} & f^{\prime \prime} (0) &=1 \\ & \vdots & & \vdots \end{array}
Then we use the definition of a Maclaurin series. 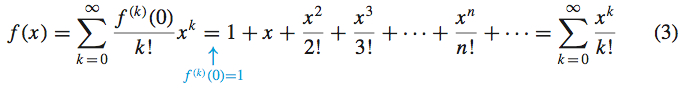
NOW WORK
614
But how can we be sure f(x) =e^{x} can be represented by a power series? We know [Example 1(a), p. 600] that the power series \sum\limits_{k\,=\,0}^{\infty }\frac{x^{k}}{k!} converges absolutely for all numbers x. But does the series \sum\limits_{k\,=\,0}^{\infty }\frac{x^{k}}{k!} converge to e^{x}? To answer these questions, we need to investigate the convergence of a Taylor series.
2 Determine the Convergence of a Taylor/Maclaurin SeriesPrinted Page 614
The conditions on the function f that guarantee that its power series representation actually converges to f are based on the Taylor polynomial P_{n}(x) of f discussed in Section 3.5 (pp. 240-241). There, we found that the Taylor polynomial P_{n}(x) of a function f whose first n derivatives are continuous on an open interval containing the number c is given by P_{n}(x) =f(c) +f^\prime (c) (x-c) +\frac{f^{\prime \prime} (c) }{2!}(x-c) ^{2}+\cdots+\,\frac{f^{(n) }(c) }{\,n!}(x-c) ^{n}
To use P_{n}(x) to approximate the function f for x close to c, we investigate the difference between f(x) and P_{n}(x), called the remainder R_{n}.
THEOREM Taylor’s Formula with Remainder
Let f be a function whose first n+1 derivatives are continuous on an open interval I containing the number c. Then for every x in I, there is a number u between x and c for which f(x) =f(c) +f^\prime (c) (x-c) +\frac{f^{\prime \prime} (c) }{2!}(x-c) ^{2}+ \cdots +\,\frac{f^{(n) }(c) }{n!}(x-c) ^{n}+R_{n}(x)
where R_{n}(x) =\frac{f^{(n+1)}(u)}{(n+1) !}(x-c) ^{n+1}
is the remainder after n terms.
The proof of this result appears in Appendix B.
The Taylor series in x-c of a function f is \sum\limits_{k\,=\,0}^{\infty }\frac{f^{(k) }(c) }{k!}(x-c)^{k}. Notice that the nth partial sum of the Taylor series in x-c of f is precisely the Taylor polynomial P_{n}(x) of f at c. If the Taylor series \sum\limits_{k\,=\,0}^{\infty }\frac{f^{(k) }(c) }{k!}(x-c) ^{k} converges to f(x), it follows that f(x) =\lim\limits_{n\rightarrow \infty }P_{n}(x)
But Taylor’s Formula with Remainder states that f(x) =P_{n}(x) +R_{n}(x)
So, if the Taylor series converges, we must have f(x) =\lim\limits_{n\rightarrow \infty }\,[P_{n}(x) +R_{n}(x)] =\lim\limits_{n\rightarrow \infty}P_{n}(x) +\lim\limits_{n\rightarrow \infty }R_{n}(x) =f(x) +\lim\limits_{n\rightarrow \infty }R_{n}(x)
That is, \lim\limits_{n\rightarrow \infty }R_{n}(x) =0.
615
THEOREM Convergence of a Taylor Series
If a function f has derivatives of all orders in an open interval I= (c-R,c+R), R>0, centered at c, and if \lim\limits_{n\rightarrow \infty }R_{n}(x)=0
for all numbers x in I, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{ll} f(x)=\sum\limits_{k\,=\,0}^{\infty }\frac{f^{(k)}(c)}{ k!}\,(x-c)^{k}&= f(c)+f^{\prime} (c)(x-c)+\frac{f^{\prime\prime} (c)}{2!} (x-c)^{2}\\ &\quad+\cdots +\frac{f^{(n)}(c)}{n!}(x-c)^{n}+\cdots \end{array}}}
for all numbers x in I.
At first glance, the convergence theorem appears simple, but in practice it is not always easy to show that \lim\limits_{n\rightarrow \infty}R_{n}(x)=0. One reason is that the term f^{(n+1)}(u), which appears in R_{n}(x), depends on n, making the limit difficult to find.
EXAMPLE 2Determining the Convergence of a Maclaurin Series
Show that 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots +\frac{x^{n}}{n!}+\cdots converges to e^{x} for every number x. That is, prove that \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!} +\cdots +\frac{x^{n}}{n!}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\frac{ x^{k}}{k!}}}
for all real numbers.
Solution To prove that 1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots =e^{x} for every number x, we need to show that \lim\limits_{n\rightarrow \infty }R_{n}(x)=0. Since f^{\,(n+1)}(x)=e^{x}, we have R_{n}(x)=\frac{f^{(n+1)}(u) x^{n+1}}{(n+1) !}=\frac{e^{u}x^{n+1}}{(n+1)!}
where u is between 0 and x. To show that \lim\limits_{n\rightarrow\infty }R_{n}(x) = 0, we consider two cases: x>0 and x<0.
NEED TO REVIEW?
The Squeeze Theorem is discussed in Section 1.4, pp. 106-107.
Case 1: When x>0, then 0<u<x, so that 1<e^{u}<e^{x} and, for every positive integer n, 0<R_{n}(x)=\frac{e^{u}x^{n+1}}{(n+1)!}<\frac{e^{x}x^{n+1}}{(n+1)!}
By the Ratio Test, the series \sum\limits_{k\,=\,\,0}^{\infty }\frac{x^{k+1}}{(k+1) !} converges for all x. It follows that \lim\limits_{n\rightarrow \infty } \frac{x^{n+1}}{(n+1) !}=0, and, therefore, \lim\limits_{n\rightarrow \infty }\frac{e^{x}x^{n+1}}{(n+1)!} =e^{x}\lim\limits_{n\rightarrow \infty }\frac{x^{n+1}}{(n+1)!}=0
By the Squeeze Theorem, \lim\limits_{n\rightarrow \infty }R_{n}(x)=0.
Case 2: When x<0, then x<u<0 and e^{x}<e^{u}<1, so that 0\leq \left\vert R_{n}(x)\right\vert =\frac{e^{u}\cdot |x|^{n+1}}{(n+1)!}< \frac{|x|^{n+1}}{(n+1)!}
616
Since \lim\limits_{n\rightarrow \infty }\frac{\vert x\vert^{n+1}}{(n+1) !}=0, by the Squeeze Theorem, \lim\limits_{n\rightarrow \infty }R_{n}(x)=0. So for all x, \lim\limits_{n\rightarrow \infty }R_{n}(x) =0. As a result, e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots +\frac{x^{n}}{n!}+\cdots =\sum_{k\,=\,0}^{\infty }\frac{x^{k}}{k!} for all numbers x.
3 Find Taylor/Maclaurin ExpansionsPrinted Page 616
EXAMPLE 3Finding the Maclaurin Expansion for f(x) = \sin x
- (a) Find the Maclaurin expansion for f(x)=\sin x.
- (b) Show that it converges to \sin x for all numbers x.
Solution (a) The value of f and its derivatives at 0 are \begin{array}{rl@{\qquad}rll} f(x) &=\sin x & f(0) &=0 \\ f^{\prime} (x) &=\cos x & f^\prime (0) &=1 \\ f^{\prime \prime} (x)&=-\sin x & f^{\prime \prime} (0) &=0 \\ f^{\prime \prime \prime}(x) &=-\cos x & f^{\prime \prime \prime} (0) &=-1 \end{array}
Higher-order derivatives follow this same pattern, so if f(x) =\sin x can be represented by a power series in x, then \begin{eqnarray*} \sin x &=& f(0) +\frac{f^{\prime} (0) }{1!}x+\frac{ f^{\prime \prime} (0) }{2!}x^{2}+\frac{f^{\prime \prime \prime} (0) }{3!}x^{3}+\cdots\,=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}- \frac{x^{7}}{7!}+\cdots\\[4pt] &=& \sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\frac{x^{2k+1}}{(2k+1) !} \end{eqnarray*}
(b) To prove that the series actually converges to \sin x for all x, we need to show that the remainders R_{2n+1}(x) and R_{2n}(x) approach zero. For R_{2n+1}(x) we have R_{2n+1}(x)=(-1)^{n+1}\frac{f^{(2n+2)}(u)\,x^{2n+2}}{(2n+2)!}
where u is between 0 and x. Since \vert f^{(2n+2)}(u)\vert = \vert \sin u \vert \leq 1 for every number u, then 0\leq \vert R\,_{2n+1}(x)\vert =\frac{\left\vert f^{(2n+2)}(u)\right\vert }{(2n+2)!}\vert x\vert ^{2n+2}\leq \frac{ \vert x\vert ^{2n+2}}{(2n+2)!}
By the Ratio Test, the series \sum\limits_{k\,=\,0}^{\infty }\frac{|x|^{2k+2} }{( 2k+2) !} converges for all x, so \lim_{n\,\dot{\rightarrow}\infty }\frac{|x|^{2n+2}}{(2n+2)!}=0
By the Squeeze Theorem, \lim\limits_{n\rightarrow \infty }\vert R_{2n+1}(x)\vert =0 and therefore \lim\limits_{n\rightarrow \infty } R_{2n+1}(x)=0 for all x.
A similar argument holds for the remainder \left\vert R_{2n}(x) \right\vert =\frac{\left\vert \cos u\right\vert x^{2n+1}}{(2n+1) !}.
We conclude that the series \sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\frac{x^{2k+1}}{(2k+1) !} converges to \sin x for all x. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sin x=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!} -\cdots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\frac{x^{2k+1}}{(2k+1)!} }}
617
The task of finding the Taylor expansion for a function f by taking successive derivatives and then showing that \lim\limits_{n\rightarrow \infty }R_{n}(x)=0 can be challenging. Consequently, it is usually easier to use a known series and properties of power series to find the Taylor series of a function f.
For example, we can find the Maclaurin expansion for f(x)=\cos x by differentiating the Maclaurin series for f(x)=\sin x.
EXAMPLE 4Finding the Maclaurin Expansion for f(x) =\cos x
Find the Maclaurin expansion for f(x) =\cos x.
Solution We apply the differentiation property of power series to the Maclaurin expansion for \sin x. \begin{eqnarray*} \frac{d}{dx}\sin x &=& \frac{d}{dx}\!\left( x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!} -\cdots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+\cdots \right) \\[5pt] &=&\frac{d}{dx}\sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\frac{x^{2k+1}}{ (2k+1) !} \end{eqnarray*}
Then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \cos x=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots +(-1)^{n}\frac{x^{2n}}{(2n)!}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\,(-1) ^{k}\frac{x^{2k}}{(2k) !}}}
for all numbers x.
NOTE
The Maclaurin expansion for f(x)=\cos x could also have been found by integrating the Maclaurin expansion for f(x)=\sin x.
We can use known Taylor expansions to obtain the power series representations of other functions. For example, if in the Maclaurin expansion for e^{x}, the variable x is replaced by -x, then f(x) =e^{-x}=1-x+\frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\cdots +(-1)^{n}\frac{x^{n}}{n!}+\cdots
for all numbers x. We use this in the next example to find the Maclaurin expansion for the hyperbolic cosine function.
EXAMPLE 5Finding the Maclaurin Expansion for f(x) =\cosh x
Find the Maclaurin expansion for f(x) =\cosh x.
Solution Since \cosh x=\frac{e^{x}+e^{-x}}{2}
its Maclaurin expansion can be found by adding corresponding terms of the Maclaurin expansions for e^{x} and e^{-x} and then dividing by 2. The result is \begin{eqnarray*} \hspace{-10pc} \cosh x &=&\frac{e^{x}+e^{-x}}{2}=\frac{\left( 1+x+\frac{x^{2}}{2!}+ \frac{x^{3}}{3!}+\cdots +\frac{x^{n}}{n!}+\cdots \right) +\left( 1-x+ \frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\cdots +(-1)^{n}\frac{x^{n}}{n!}+\cdots \right) }{2} \\[10pt] \hspace{-10pc} &=&\frac{1+1}{2}+\frac{x-x}{2}+\frac{x^{2}+x^{2}}{2\cdot 2!}+\frac{ x^{3}-x^{3}}{2\cdot 3!}+\cdots+\frac{x^{n}+(-1) ^{n}x^{n}}{ 2\cdot n!}+\cdots \end{eqnarray*}
\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \cosh x=1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+\frac{x^{6}}{6!}+\cdots + \frac{x^{2n}}{(2n)!}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\,\frac{x^{2k}}{(2k) !}}}
for all x.
NOW WORK
618
EXAMPLE 6Finding the Maclaurin Expansion for f(x) =e^{x}\cos x
Find the first five terms of the Maclaurin expansion for f(x) = e^{x}\cos x.
Solution The Maclaurin expansion for f(x) = e^{x}\cos x is obtained by multiplying the Maclaurin expansion for e^{x} by the Maclaurin expansion for \cos x. That is, e^{x}\cos x=\left( 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+ \frac{x^{5}}{5!}+\cdots \right) \left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!} -\cdots \right)
Then \begin{eqnarray*} e^{x}\cos x &=& 1 \!\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\right) +x\!\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\right) \\[5pt] && +\, \frac{x^{2}}{2!}\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\right) +\frac{x^{3}}{3!}\left( 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\right) \\[5pt] && +\, \frac{x^{4}}{4!}\left(1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots \right)+\frac{x^{5}}{5!} \left(1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\cdots\right)+\cdots \\[5pt] &=& \left( 1-\frac{x^{2}}{2}+\frac{x^{4}}{24}\right) +\left( x-\frac{x^{3}}{ 2}+\frac{x^{5}}{24}\right) +\left( \frac{x^{2}}{2}-\frac{x^{4}}{4}\right) +\left( \frac{x^{3}}{6}-\frac{x^{5}}{12}\right) \\[5pt] && +\, \frac{x^{4}}{24}+\frac{x^{5}}{120}+\cdots \\[5pt] &=& 1+x+\left( -\frac{1}{2}+\frac{1}{2}\right) x^{2}+\left( -\frac{1}{2}+ \frac{1}{6}\right) x^{3}+\left( \frac{1}{24}-\frac{1}{4}+\frac{1}{24}\right) x^{4}\\[5pt] &&+\,\left( \frac{1}{24}-\frac{1}{12}+\frac{1}{120}\right) x^{5}+\cdots \\[5pt] &=& 1+x-\frac{1}{3}x^{3}-\frac{1}{6}x^{4}-\frac{1}{30}x^{5}+\cdots \end{eqnarray*}
NOW WORK
EXAMPLE 7Finding the Taylor Expansion for f(x) =\cos x about \frac{\pi }{2}
Find the Taylor expansion for f(x) =\cos x about \frac{\pi}{2}.
Solution To express f(x) =\cos x as a Taylor expansion about \frac{\pi}{2}, we evaluate f and its derivatives at \frac{\pi}{2}. \begin{array}{rl@{\qquad}rll} f(x) &=\cos x & f\!\!\left(\frac{\pi }{2}\right)& =0 \\ f^\prime (x) &=-\sin x & f^\prime \!\!\left( \frac{\pi }{2}\right) &=-1 \\ f^{\prime \prime} (x) &=-\cos x & f^{\prime \prime} \!\!\left( \frac{\pi }{2}\right) &=0 \\ f^{\prime \prime \prime} (x) &=\sin x & f^{\prime \prime \prime} \!\!\left( \frac{\pi }{2}\right) &=1 \end{array}
For derivatives of odd order, f^{(2n+1) }\left( \frac{\pi }{2}\right) =(-1) ^{n+1}. For derivatives of even order, f^{(2n) }\left( \frac{\pi }{2}\right) =0. The Taylor expansion for f(x) =\cos x about \frac{\pi }{2} is
619
\begin{eqnarray*} f(x) &=&\cos x=f\!\!\left( \frac{\pi }{2}\right) +f^\prime \!\!\left( \frac{\pi }{2}\right) \left( x-\frac{\pi }{2}\right) +\frac{f^{\prime \prime} \!\!\left( \frac{\pi }{2}\right) }{2!}\left( x-\frac{\pi }{2}\right) ^{2}\\[6pt] &&+\, \frac{f^{\prime \prime \prime} \!\!\left( \frac{\pi }{2}\right) }{3!}\left( x-\frac{\pi }{2}\right) ^{3}+\cdots \\[6pt] &=&-\left( x-\frac{\pi }{2}\right) +\frac{1}{3!}\left( x-\frac{\pi }{2} \right) ^{3}-\frac{1}{5!}\left( x-\frac{\pi }{2}\right) ^{5}+\text{ }\cdots \\[6pt] &=& \sum\limits_{k\,=\,0}^{\infty }\frac{(-1) ^{k+1}}{(2k+1) !}\left( x-\frac{\pi }{2}\right) ^{2k+1} \end{eqnarray*}
The radius of convergence is \infty ; the interval of convergence is (-\infty ,\infty).
NOW WORK
4 Work with a Binomial SeriesPrinted Page 619
In algebra, the Binomial Theorem states that if m is a positive integer and a and b are real numbers, then \begin{eqnarray*} (a+b) ^{m} &=& a^{m}+{m\choose 1} a^{m-1}b+{m\choose 2} a^{m-2}b^{2}+\cdots+{m\choose m-2}a^{2}b^{m-2}\\ &&+{m\choose m-1} ab^{m-1}+b^{m}=\sum_{k\,=\,0}^{m}{m\choose k} a^{m-k}b^{k} \end{eqnarray*}
where {m\choose k} =\frac{m!}{k!\left( m-k\right) !}=\frac{ m( m-1 ) \,\cdots\,\left( m-k+1\right) }{k!}
In the Binomial Theorem, m is a positive integer. To generalize the result, we find a Maclaurin series for the function f(x) =(1+x) ^{m}, where m is any real number.
NEED TO REVIEW?
The Binomial Theorem is discussed in Appendix A.5, p. A-43.
EXAMPLE 8Finding the Maclaurin Expansion for f(x) =(1+x) ^{m}
Find the Maclaurin series for f(x) =(1+x) ^{m}, where m is any real number.
Solution We begin by finding the derivatives of f at 0: \begin{array}{@{\hspace{-8pc}}ll@{\qquad}rll} f(x)&=&(1+x)^{m} && f(0)&=&1 \\ f^\prime (x)&=&m(1+x)^{m-1} && f^{\prime} (0)&=&m \\ f^{\prime \prime} (x)&=&m(m-1)(1+x)^{m-2} && f^{\prime \prime} (0)&=&m(m-1) \\ \vdots & & & & & \vdots & & & &\\ f^{(n)}(x)&=&m(m-1)(m-2)\cdots (m-n+1)(1+x)^{m-n} && f^{(n)}(0) &=& m(m-1)(m-2)\,\cdots \,(m-n+1) \end{array}
The Maclaurin expansion for f is \begin{eqnarray*} (1+x)^{m} &=&1+m\,x+\frac{m(m-1)}{2!}x^{2}+\cdots \\[4pt] && +\, \frac{m(m-1)(m-2)\,\cdots \,(m-n+1)}{n!}x^{n}+\cdots \\[4pt] &=&{m\choose 0}+{m\choose 1}x+{m\choose 2}x^{2}+\cdots +{m\choose n}x^{n}+\cdots =\sum_{k\,=\,0}^{\infty }{m\choose k}\,x^{k} \end{eqnarray*}
620
where \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ {m\choose 0} =1 \quad\hbox{and}\quad {m\choose k} =\frac{m (m-1) (m-2) \,\cdots\, (m-k+1) }{k!} }}
The series \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl} (1+x) ^{m} &=&\sum\limits_{k\,=\,0}^{\infty }{m\choose k}\, x^{k}\\ &=&{1}+{m\,}x+\frac{m( m-1) }{2!}x^{2}+\frac{m\,( m-1) (m-2) }{3!}\,x^{3}+\cdots +{m\choose n}x^{n}+\cdots \end{array} }}
is called a binomial series because of its similarity in form to the Binomial Theorem, and {m\choose k} is called the binomial coefficient of {x^{k}}.
The following result, which we state without proof, gives the conditions under which the binomial series (1+x)^{m} converges.
THEOREM Convergence of a Binomial Series
The binomial series (1+x)^{m}=\sum_{k\,=\,0}^{\infty }{m\choose k}x^{k} converges
- for all x if m is a nonnegative integer. (In this case, there are only m+1 nonzero terms.)
- on the open interval (-1,1) if m\leq -1.
- on the half-open interval (-1,\,1] if -1<m<0.
- on the closed interval [-1,\,1] if m>0, but m is not an integer.
EXAMPLE 9Using a Binomial Series
Represent the function f(x) =\sqrt{x+1} as a Maclaurin series, and find its interval of convergence.
Solution Write \sqrt{x+1}=(1+x) ^{1/2} and use the binomial series with m=\frac{1}{2}. The result is \begin{eqnarray*} (1+x)^{1/2} &=& 1+\frac{1}{2}x+\frac{\left( \frac{1}{2}\right) \left( -\frac{1 }{2}\right) }{2!}\,x^{2}+\frac{\frac{1}{2}\left( -\frac{1}{2}\right) \left( -\frac{3}{2}\right) }{3!}x^{3}+\cdots \\[12pt] &=& 1+\frac{1}{2}x-\frac{1}{8} x^{2}+\frac{1}{16}x^{3} - \cdots \end{eqnarray*}
Since m=\frac{1}{2}>0 and m is not an integer, the series converges on the closed interval [-1,\,1].
NOW WORK
621
EXAMPLE 10Using a Binomial Series
Represent the function f(x)=\sin ^{-1}x by a Maclaurin series.
Solution Recall that \sin ^{-1}x=\int_{0}^{x}\frac{dt}{\sqrt{1-t^{2}}}=\int_{0}^{x}(1-t^{2})^{-1/2}dt
We write the integrand as a binomial series, with x=-t^{2} and m=-\frac{1}{2}. \begin{eqnarray*} (1-t^{2})^{-1/2} &=&1+\left( -\frac{1}{2}\right) (-t^{2}) + \frac{\left( -\frac{1}{2}\right) \left( -\frac{3}{2}\right) }{2!}(-t^{2}) ^{2}\\[8pt] && +\frac{\left( -\frac{1}{2}\right) \left( -\frac{3}{2} \right) \left( -\frac{5}{2}\right) }{3!}(-t^{2}) ^{3}+\cdots \\[8pt] &=&1+\frac{1}{2}t^{2}+\frac{3}{8}\,t^{4}+\frac{5}{16}t^{6}+\cdots \end{eqnarray*}
Now we use the integration property of a power series to obtain \begin{eqnarray*} \int_{0}^{x}\frac{dt}{\sqrt{1-t^{2}}} &=&\int_{0}^{x}\left( 1+\frac{1}{2} t^{2}+\frac{3}{8}\,t^{4}+\frac{5}{16}t^{6}+\cdots \right)\,dt \\ \sin ^{-1}x &=& x+\left( \frac{1}{2}\right) \left( \frac{x^{3}}{3}\right) +\left( \frac{3}{8}\right) \left( \frac{x^{5}}{5}\right) +\left( \frac{5}{16} \right) \left( \frac{x^{7}}{7}\right) +\cdots \\ &=& x+\frac{x^{3}}{6}+\frac{3}{40}x^{5}+\frac{5}{112}x^{7}+\cdots \end{eqnarray*}
In Problem 57, you are asked to show that the interval of convergence is [-1,1].
Summary
| Series | Comment |
|---|---|
| \frac{1}{1-x}=\sum\limits_{k\,=\,0}^{\infty}x^{k}=1+x+x^{2}+x^{3}+\cdots | Converges for \vert x\vert <1. |
| \tan ^{-1}x=\sum\limits_{k\,=\,0}^{\infty }(-1) ^{k}\frac{x^{2k+1}}{2k+1}=x-\frac{x^{3}}{3}+\frac{x^{5}}{5} -\,\cdots | Converges on the interval [-1,\,1]. |
| e^{x}=\sum\limits_{k\,=\,0}^{\infty }\frac{x^{k}}{k!}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots | Converges for all real numbers x. |
| \sin x=\sum\limits_{k\,=\,0}^{\infty }\frac{(-1)^{k}\,x^{2k+1}}{(2k+1)!}=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots | Converges for all real numbers x. |
| \cos x=\sum\limits_{k\,=\,0}^{\infty }\frac{(-1)^{k}x^{2k}}{(2k)!}=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots | Converges for all real numbers x. |
| \ln (1+x)=\sum\limits_{k\,=\,0}^{\infty }\frac{(-1)^{k}\,x^{k+1}}{k+1} | Converges on the interval (-1,\,1]. |
| (1+x)^{m}=\sum\limits_{k\,=\,0}^{\infty }{m\choose k} \,x^{k} | For convergence, see the theorem on page 620. |
