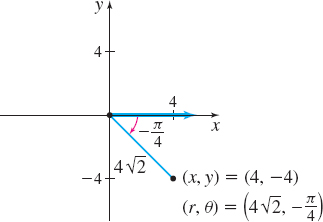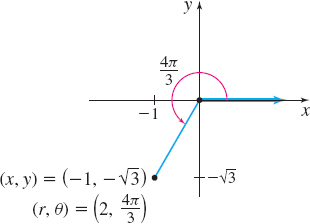Parametric Equations; Polar Equations

9.4 Polar Coordinates
Printed Page 661

OBJECTIVES

When you finish this section, you should be able to:

Plot points using polar coordinates (p. 661)
Convert between rectangular coordinates and polar coordinates (p. 664)
Identify and graph polar equations (p. 666)

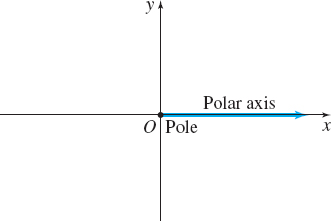
In a rectangular coordinate system, there are two perpendicular axes, one horizontal (the $x$ -axis) and one vertical (the $y$ -axis). The point of intersection of the axes is the origin and is labeled $O.$ A point is represented by a pair of numbers $(x,y)$ , where $x$ and $y$ equal the signed distance of the point from the $y$ -axis and the $x$ -axis, respectively. A polar coordinate system is constructed by selecting a point $O$ , called the pole, and a ray with its vertex at the pole, called the polar axis. It is customary to have the pole coincide with the origin and the polar axis coincide with the positive $x$ -axis of the rectangular coordinate system, as shown in Figure 24.

1 Plot Points Using Polar Coordinates
Printed Page 661

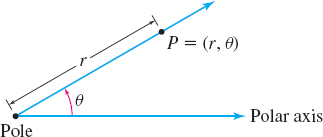
A point $P$ in the polar coordinate system is represented by an ordered pair of numbers $(r,\theta )$ , called the polar coordinates of $P.$ If $r>0,$ then $r$ is the distance of the point from the pole (the origin), and $\theta$ is an angle (measured in radians or degrees) whose initial side is the polar axis (the positive $x$ -axis) and whose terminal side is a ray from the pole through the point $P.$ See Figure 25.

Figure 25 Polar Coordinates

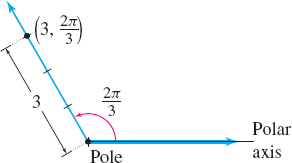
As an example, suppose the polar coordinates of a point $P$ are $\left( 3,\dfrac{2\pi }{3}\right)$ . We locate $P$ by drawing an angle of $\dfrac{2\pi }{3}$ radians with its vertex at the pole and its initial side along the polar axis. Then $P$ is the point on the terminal side of the angle that is $3$ units from the pole. See Figure 26.

Figure 26

662

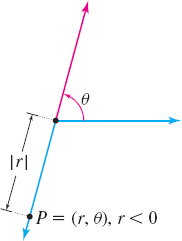
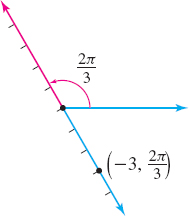
If $r=0$ , then the point $P=( 0,\theta )$ is at the pole for any $\theta .$ If $r<0,$ the location of the point $P$ is not on the terminal side of $\theta .$ Instead, $P$ is on the extension through the pole of the ray forming the terminal side of $\theta$ and at a distance $\vert r\vert$ from the pole. See Figure 27. So, the point $\left( -3,\,\dfrac{2\pi }{3}\right)$ is located $3$ units from the pole on the extension through the pole of the ray that forms the angle $\dfrac{2\pi }{3}$ with the polar axis. See Figure 28.

NOTE

The points $(r,\theta)$ and $(-r,\theta)$ are reflections about the pole.

Figure 27

Figure 28

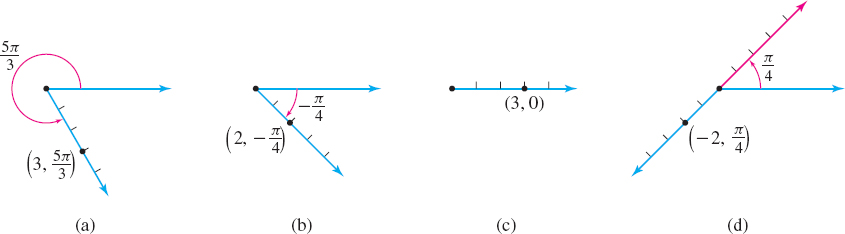
EXAMPLE 1Plotting Points Using Polar Coordinates

Plot the points with the following polar coordinates:

(a) $\left( 3,\dfrac{5\pi }{3}\right)$

(b) $\left( 2,-\dfrac{\pi }{4}\right)$

(c) $( 3,0)$

(d) $\left( -2,\,\dfrac{\pi }{4}\right)$

Solution Figure 29 shows the points.

Figure 29

NOW WORK

Problems 17 and 23.

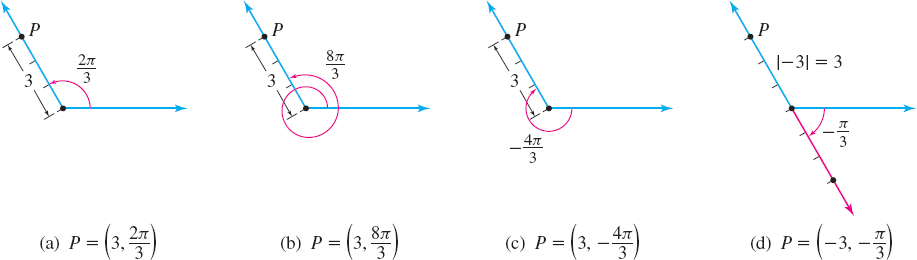
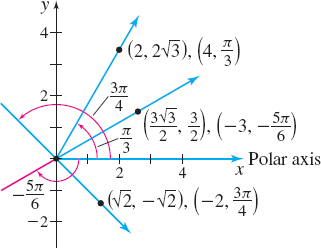
The polar coordinates $\left( 3,\dfrac{2\pi }{3}\right)$ of the point $P$ shown in Figure 30(a) on page 663 are one of many possible polar coordinates of $P$ . For example, since the angles $\dfrac{8\pi }{3}$ and $-\dfrac{4\pi }{3}$ have the same terminal side as the angle $\dfrac{2\pi }{3}$ , the point $P$ can be represented by any of the polar coordinates $\left( 3,\dfrac{2\pi }{3}\right),\;\left( 3,\dfrac{8\pi }{3}\right)$ , and $\left( 3,-\dfrac{4\pi }{3}\right)$ , as shown in Figures 30(a)–(c). The point $\left( 3,\dfrac{2\pi }{3}\right)$ can also be represented by the polar coordinates $\left( -3,-\dfrac{\pi }{3}\right)$ , as illustrated in Figure 30(d).

663

Figure 30

So, there is a major difference between rectangular and polar coordinate systems. In a rectangular system, each point in the plane corresponds to exactly one pair of rectangular coordinates; in a polar coordinate system, every point in the plane can be represented by infinitely many polar coordinates.

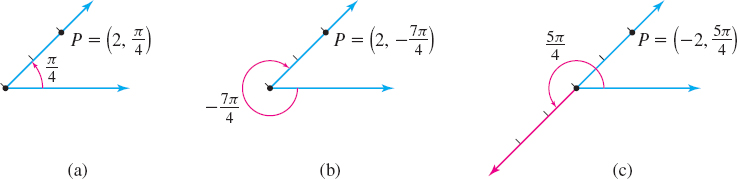
EXAMPLE 2Plotting a Point Using Polar Coordinates

Plot the point $P$ whose polar coordinates are $\left( -2,-\dfrac{3\pi }{4}\right)$ . Then find three other polar coordinates of the same point with the properties:

(a) $r>0$ and $0<\theta <2\pi$

(b) $r>0$ and $-2\pi <\theta <0$

(c) $r<0$ and $0<\theta <2\pi$

Figure 31

The point $\left( -2,-\dfrac{3\pi }{4}\right)$ is located by first drawing the angle $-\dfrac{3\pi }{4}$ . Then $P$ is on the extension of the terminal side of $\theta$ through the pole at a distance $2$ units from the pole, as shown in Figure 31.

(a) The point $P=( r,\theta ) ,$ $r>0,$ $0<\theta<2\pi$ is $\left( 2,\dfrac{\pi }{4}\right)$ , as shown in Figure 32(a).

(b) The point $P=( r,\theta ) ,$ $r>0,$ $-2\pi <\theta<0$ is $\left( 2,-\dfrac{7\pi }{4}\right)$ , as shown in Figure 32(b).

(c) The point $P=( r,\theta ) ,$ $r<0,$ $0<\theta<2\pi$ is $\left( -2,\dfrac{5\pi }{4}\right)$ , as shown in Figure 32(c).

Figure 32

NOW WORK

Problem 25.

Summary

A point $P$ with polar coordinates $(r,\theta )$ also can be represented by $\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ ( r,\theta +2n\pi ) \qquad \hbox{or} \qquad ( -r, \theta+ ( 2n+1) \pi )\quad n \hbox{ is an integer } }}$
The polar coordinates of the pole are $(0,\,\theta )$ , where $\theta$ is any angle.

2 Convert Between Rectangular Coordinates and Polar Coordinates
Printed Page 664

664

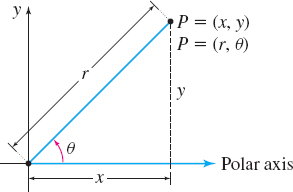
It is sometimes useful to transform coordinates or equations in rectangular form into polar form, or vice versa. To do this, recall that the origin in the rectangular coordinate system coincides with the pole in the polar coordinate system and the positive $x$ -axis in the rectangular system coincides with the polar axis in the polar system. The positive $y$ -axis in the rectangular system is the ray $\theta =\dfrac{\pi }{2}$ in the polar system.

Figure 33

Suppose a point $P$ has the polar coordinates $(r,\theta )$ and the rectangular coordinates ( $x,y$ ), as shown in Figure 33. If $r>0$ , then $P$ is on the terminal side of $\theta ,$ and $\begin{equation*} \cos \theta =\frac{x}{r}\qquad \hbox{and}\qquad \sin \theta =\frac{y}{r} \end{equation*}$

If $r<0$ , then $P=(r,\theta )$ can be represented as $(-r,\pi +\theta )$ , where $-r>0$ . Since $\begin{equation*} \cos ( \theta +\pi ) =-\cos \theta =\dfrac{x}{-r}\qquad \hbox{and}\qquad \sin ( \theta +\pi ) =-\sin \theta =\dfrac{y}{-r} \end{equation*}$

then, whether $r>0$ or $r<0$ , $\begin{equation*} x=r\cos \theta \qquad\hbox{and}\qquad y=r\sin \theta \end{equation*}$

If $r=0$ , then $P$ is the pole and the same relationships hold.

NEED TO REVIEW?

The definitions of the trigonometric functions and their properties are discussed in Appendix A.4, pp. A-27 to A-32.

THEOREM Conversion from Polar Coordinates to Rectangular Coordinates

If $P$ is a point with polar coordinates $( r,\theta ) ,$ then the rectangular coordinates $( x, y)$ of $P$ are given by $\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ x=r\cos \theta\qquad \hbox{and} \qquad y=r\sin \theta }}$

EXAMPLE 3Converting from Polar Coordinates to Rectangular Coordinates

Find the rectangular coordinates of each point whose polar coordinates are:

(a) $\left( 4,\dfrac{\pi }{3}\right)$

(b) $\left( -2,\dfrac{3\pi }{4}\right)$

(c) $\left(-3,-\dfrac{5\pi }{6}\right)$

(a) We use the equations $x=r\cos \theta$ and $y=r\sin \theta$ with $r=4$ and $\theta =\dfrac{\pi }{3}.$ $x=4\cos \dfrac{\pi }{3}=4\left( \dfrac{1}{2}\right) =2 \qquad \hbox{and} \qquad y=4\sin \dfrac{\pi }{3}=4\left( \dfrac{\sqrt{3}}{2}\right) =2\sqrt{3}$

The rectangular coordinates are $(2,2\sqrt{3}).$

(b) We use the equations $x=r\cos \theta$ and $y=r\sin \theta$ with $r=-2$ and $\theta =\dfrac{3\pi }{4}.$ $x=-2\cos \dfrac{3\pi }{4}=-2\left(-\dfrac{\sqrt{2}}{2}\right) =\sqrt{2} \quad\hbox{and}\quad y=-2\sin \dfrac{3\pi }{4}=-2\left( \dfrac{\sqrt{2}}{2}\right) =-\sqrt{2}$

The rectangular coordinates are $( \sqrt{2},-\sqrt{2}) .$

(c) We use the equations $x=r\cos \theta$ and $y=r\sin \theta$ with $r=-3$ and $\theta =-\dfrac{5\pi }{6}.$ $\begin{eqnarray*} x&=&-3\cos \left( -\dfrac{5\pi }{6}\right) =-3\left( -\dfrac{\sqrt{3}}{2} \right) =\dfrac{3\sqrt{3}}{2}\;\hbox{}\; \\[4pt] y&=&-3\sin \left( -\dfrac{5\pi }{6}\right) =-3\left( -\dfrac{1}{2}\right) =\dfrac{3}{2} \end{eqnarray*}$

Figure 34

The rectangular coordinates are $\left( \dfrac{3\sqrt{3}}{2},\dfrac{3}{2}\right)$ .

665

The points $\left( 4,\dfrac{\pi }{3}\right),\;\left( -2,\dfrac{3\pi }{4}\right)$ , and $\left( -3,-\dfrac{5\pi }{6}\right)$ and the points $(2,2\sqrt{3}),\;( \sqrt{2},-\sqrt{2}) ,$ and $\left( \dfrac{3\sqrt{3}}{2},\dfrac{3}{2}\right)$ are graphed in their respective coordinate systems in Figure 34.

NOW WORK

Problems 33 and 39.

Now suppose $P$ has the rectangular coordinates $(x,y)$ . To represent $P$ in polar coordinates, refer again to Figure 33. The point $P$ lies on a circle with radius $r$ and center at $(0,0)$ , so $x^{2}+y^{2}=r^{2}$ . Since $\tan \theta =\dfrac{y}{x}$ , if $x\neq 0$ , we have $\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{r^{2}=x^{2}+y^{2} \qquad \hbox{and} \qquad \tan \theta =\dfrac{y}{x}\;x\neq 0} }$

If $x=0$ , the point $P=( x,y)$ is on the $y$ -axis. So, $r=y$ and $\theta =\dfrac{\pi }{2}$ .

Conversion from Rectangular Coordinates to Polar Coordinates

If $P$ is any point in the plane with rectangular coordinates $(x,y)$ , the polar coordinates $\left( r,\,\theta \right)$ of $P$ are given by $\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ r=\sqrt{x^{2}+y^{2}}\qquad \hbox{and} \qquad \tan \theta =\dfrac{y}{x}\;\hbox{if}\ x\neq 0 }}$ $\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ r=y\qquad \hbox{and} \qquad \theta =\dfrac{\pi }{2}\;\hbox{if}\ x=0 }}$

Be careful when applying this theorem. If $x\neq 0,$ $\tan \theta = \dfrac{y}{x}$ and $\theta =\tan ^{-1}\dfrac{y}{x},$ $-\dfrac{\pi }{2}<\theta<\dfrac{\pi }{2},$ placing $\theta$ in quadrants I or IV. If the point lies in quadrant II or III, we must find $\tan ^{-1}\left( \dfrac{y}{x}\right)$ in quadrant I or IV, respectively, and then add $\pi$ to the result. It is advisable to plot the point $( x,y)$ at the start to identify the quadrant that contains the point.

NEED TO REVIEW?

The inverse tangent function is discussed in Section P.7, pp. 58-60.

EXAMPLE 4Converting from Rectangular Coordinates to Polar Coordinates

Find polar coordinates of each point whose rectangular coordinates are:

(a) $(4,-4)$

(b) $( -1,-\sqrt{3})$

(c) $( 4,-1)$

Figure 35

(a) The point $( 4,-4)$ , plotted in Figure 35, is in quadrant IV. The distance from the pole to the point $(4,-4)$ is $\begin{equation*} r=\sqrt{x^{2}+y^{2}}=\sqrt{4^{2}+( -4) ^{2}}=\sqrt{32}=4\sqrt{2} \end{equation*}$

Since the point $( 4,-4)$ is in quadrant IV, $-\dfrac{\pi }{2} <\theta <0.$ So, $\begin{equation*} \theta =\tan ^{-1}\left( \dfrac{y}{x}\right) =\tan ^{-1}\left( \dfrac{-4}{4}\right) =\tan ^{-1}( -1) =-\dfrac{\pi }{4} \end{equation*}$

666

A pair of polar coordinates for this point is $\left( 4\sqrt{2},-\dfrac{\pi }{4}\right) .$ Other possible representations include $\left( -4\sqrt{2}, \dfrac{3\pi }{4}\right)$ and $\left( 4\sqrt{2},\dfrac{7\pi }{4}\right)$ .

Figure 36

(b) The point $( -1,-\sqrt{3}) ,$ plotted in Figure 36, is in quadrant III. The distance from the pole to the point $( -1,-\sqrt{3})$ is $\begin{equation*} r=\sqrt{( -1) ^{2}+( -\sqrt{3}) ^{2}}=\sqrt{1+3}=2 \end{equation*}$

Since the point $( -1,-\sqrt{3})$ lies in quadrant III and the inverse tangent function gives an angle in quadrant I, we add $\pi$ to $\tan ^{-1}\left( \dfrac{y}{x}\right)$ to obtain an angle in quadrant III. $\begin{equation*} \theta =\tan ^{-1}\left( \dfrac{-\sqrt{3}}{-1}\right) +\pi =\tan ^{-1}( \sqrt{3}) +\pi =\dfrac{\pi }{3}+\pi =\dfrac{4\pi }{3} \end{equation*}$

A pair of polar coordinates for the point is $\left( 2,\dfrac{4\pi }{3} \right)$ . Other possible representations include $\left( -2,\dfrac{\pi }{3} \right)$ and $\left( 2,-\dfrac{2\pi }{3}\right)$ .

Figure 37

(c) The point $\left( 4,-1\right) ,$ plotted in Figure 37, lies in quadrant IV. The distance from the pole to the point $( 4,-1)$ is $\begin{equation*} r=\sqrt{x^{2}+y^{2}}=\sqrt{4^{2}+( -1) ^{2}}=\sqrt{17} \end{equation*}$

Since the point $( 4,-1)$ is in quadrant IV, $-\dfrac{\pi }{2}<\theta <0.$ So, $\begin{equation*} \theta =\tan ^{-1}\left( \dfrac{y}{x}\right) =\tan ^{-1}\left( \dfrac{-1}{4} \right) \approx -0.245\hbox{ radians} \end{equation*}$

A pair of polar coordinates for this point is $( \sqrt{17} ,-0.245) .$ Other possible representations for the point include $\left( \sqrt{17} ,\tan ^{-1}\left( -\dfrac{1}{4}\right) +2\pi \right) \approx ( \sqrt{17} ,6.038)$ and $\left( -\sqrt{17},\tan ^{-1}\left( -\dfrac{1}{4}\right) +\pi \right) \approx ( -\sqrt{17},2.897)$ .

NOW WORK

Problems 41 and 47.

3 Identify and Graph Polar Equations
Printed Page 666

Figure 38 Polar grid

Just as a rectangular grid is used to plot points given by rectangular coordinates, a polar grid is used to plot points given by polar coordinates. A polar grid consists of concentric circles centered at the pole and of rays with vertices at the pole, as shown in Figure 38. An equation whose variables are polar coordinates is called a polar equation, and the graph of a polar equation is the set of all points for which at least one of the polar coordinate representations satisfies the equation.

Polar equations of circles with their center at the pole, lines containing the pole, horizontal and vertical lines, and circles containing the pole have simple polar equations. In Section 9.5, we graph other important polar equations.

There are occasions when geometry is all that is needed to graph a polar equation. But usually other methods are required. One method used to graph polar equations is to convert the equation to rectangular coordinates. In the discussion that follows, $(x,y)$ represents the rectangular coordinates of a point $P$ , and $(r,\theta )$ represents polar coordinates of the point $P.$

667

EXAMPLE 5Identifying and Graphing a Polar Equation

Identify and graph each equation:

(a) $r=3$

(b) $\theta =\dfrac{\pi }{4}$

Figure 39

$r=3$ or

$x^{2} + y^{2} = 9$ .

(a) If $r$ is fixed at $3$ and $\theta$ is allowed to vary, the graph is a circle with its center at the pole and radius 3, as shown in Figure 39. To confirm this, we convert the polar equation $r=3$ to a rectangular equation. $\begin{array}{rcl@{\qquad}l} r &=&3 \\ r^{2} &=&9\quad{\color{#0066A7}{{\hbox{Square both sides.}}}} \\ x^{2}+y^{2} &=&9\quad{\color{#0066A7}{{\hbox{$r^{2} =x^{2} +y^{2}$}}}} \end{array}$

Figure 40

$\theta =\dfrac{\pi }{4}$ or

$y=x$ .

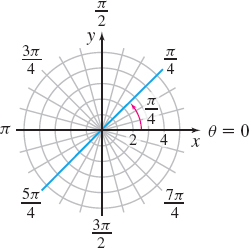
(b) If $\theta$ is fixed at $\dfrac{\pi }{4}$ and $r$ is allowed to vary, the result is a line containing the pole, making an angle of $\dfrac{\pi }{4}$ with the polar axis. That is, the graph of $\theta =\dfrac{\pi }{4}$ is a line containing the pole with slope $\tan \theta =\tan \dfrac{\pi }{4}=1$ , as shown in Figure 40. To confirm this, we convert the polar equation to a rectangular equation. $\begin{array}{rcl} \theta &=&\dfrac{\pi }{4} \\ \tan \theta &=&\tan \dfrac{\pi }{4} \\ \dfrac{y}{x} &=&1 \\ y &=&x \end{array}$

NOW WORK

Problems 51 and 61.

EXAMPLE 6Identifying and Graphing Polar Equations

Identify and graph the equations:

(a) $r\sin \theta =2$

(b) $r=4\sin \theta$

Figure 41

$r\sin \theta =2$ or

$y=2$ .

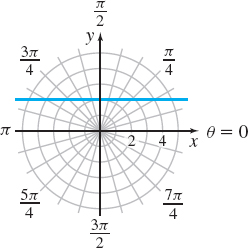
(a) Here, both $r$ and $\theta$ are allowed to vary, so the graph of the equation is not as obvious. If we use the fact that $y=r\sin \theta ,$ the equation $r\sin \theta =2$ becomes $y=2.$ So, the graph of $r\sin \theta =2$ is the horizontal line $y=2$ that lies $2$ units above the pole, as shown in Figure 41.

(b) To convert the equation $r=4\sin \theta$ to rectangular coordinates, we multiply the equation by $r$ to obtain $\begin{equation*} r^{2}=4r\sin \theta \end{equation*}$

Now we use the formulas $r^{2}=x^{2}+y^{2}$ and $y=r\sin \theta$ . Then $\begin{array}{rcl@{\qquad}l} r^{2} &=&4r\sin \theta \\ x^{2}+y^{2} &=&4y & {\color{#0066A7}{{\hbox{$r^{2} =x^{2} + y^{2},\;r\sin \theta =y$}}}} \\ x^{2}+(y^{2}-4y) &=&0 \\ x^{2}+\left( y^{2}-4y+4\right) &=&4 & {\color{#0066A7}{{\hbox{Complete the square in $y$.}}}} \\ x^{2}+(y-2)^{2} &=&4 & {\color{#0066A7}{{\hbox{Factor.}}}} \end{array}$

Figure 42

$r=4\sin \theta$ or

$x^{2}+(y-2)^{2}=4$ .

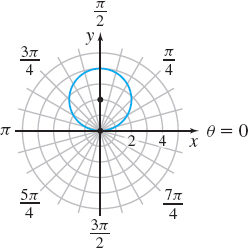
This is the standard form of the equation of a circle with its center at the point $( 0,2)$ and radius $2$ in rectangular coordinates. See Figure 42. Notice that the circle passes through the pole.

NOW WORK

Problems 65 and 67.

Table 1 summarizes and extends the results of Examples 5 and 6.

Table 1: TABLE 1

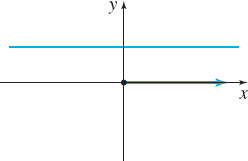
Description	Line passing through the pole making an angle $\alpha$ with the polar axis	Vertical line	Horizontal line
Rectangular equation	$y=(\tan \alpha)x$	$x=a$	$y=b$
Polar equation	$\theta = \alpha$	$r \cos \theta = a$	$r \sin \theta =b$
Typical graph
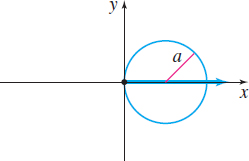
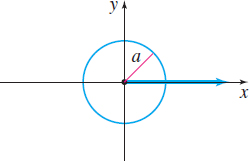
Description	Circle, center at the pole, radius $a$	Circle, passing through the pole, tangent to the line $\theta=\dfrac{\pi}{2}$ , center on the polar axis, radius $a$	Circle, passing through the pole, tangent to the polar axis, center on the line $\theta = \dfrac{\pi}{2}$ , radius $a$
Rectangular equation	$x^2+y^2=a^2,\;a>0$	$x^2+y^2=\pm 2ax,\;a>0$	$x^2+y^2=\pm 2ay,\;a>0$
Polar equation	$r=a,\;a>0$	$r=\pm 2a \cos\theta,\;a>0$	$r=\pm 2a \sin\theta,\;a>0$
Typical graph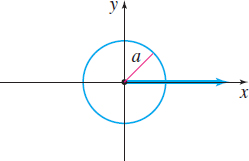